1.1. Expresión que carece de sentido (Ex.Nov/12)
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== ==Solución== Categoría:Problemas de vectores libres (G.I.T.I.)') |
(→Enunciado) |
||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| + | Si <math>\,\vec{a}</math>, <math>\vec{b}</math>, <math>\vec{c}\,</math> y <math>\,\vec{d}\,</math> son vectores | ||
| + | libres, y <math>\,\lambda\,</math> es un escalar, ¿cuál de las cuatro siguientes | ||
| + | expresiones carece de sentido en el álgebra vectorial? | ||
| + | :(1) <math>\frac{\lambda\,\vec{a}\cdot\vec{b}}{|\vec{c}\times\vec{d}\,|}</math> | ||
| + | |||
| + | :(2) <math>\frac{\vec{a}\times\vec{b}}{(\vec{c}\cdot\vec{d}\,)}</math> | ||
| + | |||
| + | :(3) <math>\vec{a}\cdot[\vec{b}\times(\vec{c}\cdot\vec{d}\,)]</math> | ||
| + | |||
| + | :(4) <math>\vec{a}\times[(\vec{b}\times\vec{c}\,)+\lambda\,\vec{d}\,\,]</math> | ||
==Solución== | ==Solución== | ||
Revisión de 18:20 13 sep 2013
1 Enunciado
Si 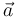 ,
,  ,
, 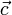 y
y 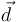 son vectores
libres, y
son vectores
libres, y 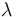 es un escalar, ¿cuál de las cuatro siguientes
expresiones carece de sentido en el álgebra vectorial?
es un escalar, ¿cuál de las cuatro siguientes
expresiones carece de sentido en el álgebra vectorial?
- (1)
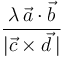
- (2)
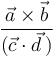
- (3)
![\vec{a}\cdot[\vec{b}\times(\vec{c}\cdot\vec{d}\,)]](/wiki/images/math/c/1/3/c132a4a94ea89ad17bc716c7276bec3b.png)
- (4)
![\vec{a}\times[(\vec{b}\times\vec{c}\,)+\lambda\,\vec{d}\,\,]](/wiki/images/math/5/7/6/576e6b5b251e8d331940a9f5616e8ec0.png)





