Consumo de un coche de gasolina
De Laplace
m |
|||
| Línea 24: | Línea 24: | ||
==Consumo== | ==Consumo== | ||
| + | Para recorrer 100\,km a una velocidad de 160\,km/h tarda un tiempo | ||
| + | |||
| + | <center><math>T = \frac{s}{v}=\frac{100\,\mathrm{km}}{160\,\mathrm{km}/\mathrm{h}}\times \frac{3600\,\mathrm{s}}{1\,\mathrm{h}}=2250\,\mathrm{s}</math></center> | ||
| + | |||
| + | por lo que en ese tiempo requerirá una cantidad de calor | ||
| + | |||
| + | <center><math>Q_\mathrm{in}=\dot{Q}_\mathrm{in}T = \frac{260\,\mathrm{kJ}}{\mathrm{s}}\times 2250\,\mathrm{s}=585\,\mathrm{MJ}</math></center> | ||
| + | |||
| + | Puesto que un litro de gasolina genera 33 MJ, el consumo será | ||
| + | |||
| + | <center><math>c = \frac{585\,\mathrm{MJ}}{33\,\mathrm{MJ}/\mathrm{l}} = 17.7\,\mathrm{l}</math></center> | ||
| + | |||
| + | Este consumo es muy superior al que realmente realiza un coche. La razón es que un automóvil muy pocas veces trabaja a potencia máxima. Solo en pendientes muy inclinadas o grandes cargas se emplea el motor a fondo. | ||
[[Categoría:Problemas de máquinas térmicas (GIE)]] | [[Categoría:Problemas de máquinas térmicas (GIE)]] | ||
última version al 17:13 2 sep 2013
1 Enunciado
Un Seat León TSI 2.0 amarillo posee una potencia de 210 CV y una relación de compresión de 9.6.
- ¿Cuánto calor hace falta producir por segundo para circular a la máxima potencia?
- ¿Cuánta gasolina consumiría a los 100 km, recorridos a máxima potencia a 160 km/h?
Datos: 1 CV = 0.736 kW; Rendimiento de un ciclo Otto ideal: η = 1 − 1 / rγ − 1; Calor generado en la combustión de 1 litro de gasolina: 33000 kJ.
2 Calor necesario
La relación entre el calor que entra y el trabajo que sale la da el rendimiento
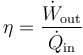
Despejando de aquí
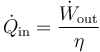
Si suponemos que el rendimiento lo da un ciclo Otto ideal
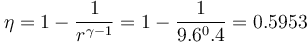
y de aquí nos da el calor necesario por segundo
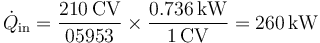
3 Consumo
Para recorrer 100\,km a una velocidad de 160\,km/h tarda un tiempo
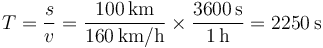
por lo que en ese tiempo requerirá una cantidad de calor
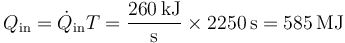
Puesto que un litro de gasolina genera 33 MJ, el consumo será
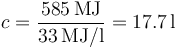
Este consumo es muy superior al que realmente realiza un coche. La razón es que un automóvil muy pocas veces trabaja a potencia máxima. Solo en pendientes muy inclinadas o grandes cargas se emplea el motor a fondo.





