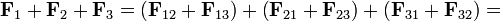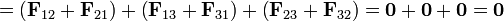Tres cargas en un triángulo equilátero
De Laplace
(→Cargas iguales y positivas) |
(→Solución) |
||
| Línea 21: | Línea 21: | ||
A su vez la fuerza entre cada par de cargas tiene la misma magnitud, ya que las cargas son todas iguales, y también lo son las distancias entre ellas | A su vez la fuerza entre cada par de cargas tiene la misma magnitud, ya que las cargas son todas iguales, y también lo son las distancias entre ellas | ||
| - | <center><math>F_{ik}=\left|\mathbf{F}_{ik}\right| = \frac{q^2}{4\pi\varepsilon_0 a^2}</math></center> | + | <center><math>F_{ik}=\left|\mathbf{F}_{ik}\right| = \frac{q^2}{4\pi\varepsilon_0 a^2} \simeq 90\,\mathrm{N}</math></center> |
Para hallar la resultante sobre una de las cargas (a la que llamaremos “3”) observamos que <math>\mathbf{F}_{31}</math> y <math>\mathbf{F}_{32}</math> se encuentran sobre los lados de un rombo, formando un ángulo de <math>\pi/6</math> con su diagonal, que a su vez va en la dirección de la línea que pasa por el centro del triángulo y por la carga 3. La resultante viene dada por esta diagonal y tiene por módulo | Para hallar la resultante sobre una de las cargas (a la que llamaremos “3”) observamos que <math>\mathbf{F}_{31}</math> y <math>\mathbf{F}_{32}</math> se encuentran sobre los lados de un rombo, formando un ángulo de <math>\pi/6</math> con su diagonal, que a su vez va en la dirección de la línea que pasa por el centro del triángulo y por la carga 3. La resultante viene dada por esta diagonal y tiene por módulo | ||
| - | <center><math>F_3 = 2F_{ik}\cos\left(\frac{pi}{6}\right) = \sqrt{3}F_{ik} = \frac{\sqrt{3}q^2}{4\pi\varepsilon_0 a^2}</math></center> | + | <center><math>F_3 = 2F_{ik}\cos\left(\frac{pi}{6}\right) = \sqrt{3}F_{ik} = \frac{\sqrt{3}q^2}{4\pi\varepsilon_0 a^2}\simeq 156\,\mathrm{N}</math></center> |
en cuanto a su dirección y sentido, va en la dirección radial desde el centro de la carga. | en cuanto a su dirección y sentido, va en la dirección radial desde el centro de la carga. | ||
Revisión de 09:48 28 nov 2008
Contenido |
1 Enunciado
Tres cargas q1, q2 y q3, se encuentran en los vértices de un triángulo equilátero de lado a = 1cm. Determine la fuerza sobre cada carga cuando:
-
.
-
.
-
, 
.
- ,
.
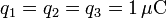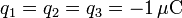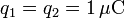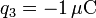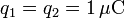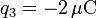2 Solución
En cada caso, la fuerza sobre cada carga es la suma vectorial de las fuerzas que cada una de las otras cargas producen sobre ella.
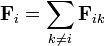
A su vez, la fuerza entre dos cargas viene dada por la ley de Coulomb
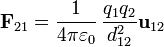
2.1 Cargas iguales y positivas
En el primer caso, por la simetría del sistema, es evidente que las tres cargas van a estar sometidas a una fuerza de la misma magnitud (aunque de dirección y sentido distinto; esto es, las tres cargas no experimentan la misma fuerza).
A su vez la fuerza entre cada par de cargas tiene la misma magnitud, ya que las cargas son todas iguales, y también lo son las distancias entre ellas
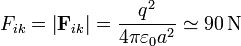
Para hallar la resultante sobre una de las cargas (a la que llamaremos “3”) observamos que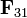 
y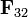 
se encuentran sobre los lados de un rombo, formando un ángulo de π / 6 con su diagonal, que a su vez va en la dirección de la línea que pasa por el centro del triángulo y por la carga 3. La resultante viene dada por esta diagonal y tiene por módulo
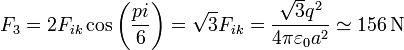
en cuanto a su dirección y sentido, va en la dirección radial desde el centro de la carga.
Este razonamiento es válido para cada una de las cargas del triángulo. Las tres fuerzas tienen el mismo módulo y su dirección y sentido son radiales hacia afuera del triángulo.
Puede comprobarse que la suma vectorial de las tres fuerzas es nula, tanto geométricamente como analíticamente
