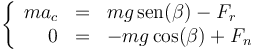Entrar Página Discusión Historial Go to the site toolbox

Cilindro que rueda por una pendiente

De Laplace

(Diferencias entre revisiones)
(→Relación entre aceleraciones)
Línea 38: Línea 38:
==Aceleración del CM==
==Aceleración del CM==
 +
El valor de la aceleración lo podemos obtener a partir de las fuerzas o mediante razonamientos energéticos.
 +
===A partir de las fuerzas===
 +
Las leyes de la dinámica para un sólido nos dan la ecuación
 +
 +
<center><math>\sum_i\vec{F}_i = M\vec{a}_C</math></center>
 +
 +
siendo las fuerzas que se aplican sobre el cilindro
 +
 +
* El peso
 +
 +
<center><math>m\vec{g}=mg\,\mathrm{sen}(\beta)\vec{\imath}-mg\cos(\beta)\vec{\jmath}</math></center>
 +
* La fuerza normal
 +
 +
<center><math>\vec{F}_n = F_n\vec{\jmath}</math></center>
 +
 +
* La fuerza de rozamiento
 +
 +
<center><math>\vec{F}_r = -F_r\vec{\imath}</math></center>
 +
 +
lo que llevado a la segunda ley de Newton y separado en componentes nos da las relaciones
 +
 +
<center><math>\left\{\begin{array}{rcl} ma_c & = & mg\,\mathrm{sen}(\beta)-F_r \\ 0 & = & -mg\cos(\beta)+F_n\end{array}\right.</math></center>
==Condición sobre el rozamiento==
==Condición sobre el rozamiento==
[[Categoría:Problemas de dinámica del sólido rígido (GIE)]]
[[Categoría:Problemas de dinámica del sólido rígido (GIE)]]

Revisión de 18:53 25 jun 2013

Contenido

1 Enunciado

Un cilindro macizo homogéneo de masa M y radio R rueda sin deslizar por un plano inclinado un ángulo β. El coeficiente de rozamiento estático entre el plano y el cilindro es μ. El rozamiento por rodadura es despreciable.

  1. ¿Qué relación existe entre la aceleración angular del sólido y la lineal de su centro de masas?
  2. ¿Cuánto vale, en módulo, la aceleración del centro de masas del cilindro?
  3. ¿Qué condición debe cumplir la inclinación que debe tener el plano si no se quiere que el cilindro empiece a deslizar?

2 Relación entre aceleraciones

Aquí hay que tener cuidado con no usar las fórmulas de rotación de una partícula, sino las de un sólido.

Puesto que el cilindro desciende rodando, el movimiento es plano y podemos representarlo como un círculo que rueda por una línea inclinada. Sea C el centro del disco y A el punto de contacto del disco sobre el suelo en un instante dado. Aplicando la ´formula del campo de velocidades de un sólido, la velocidad de A se puede escribir

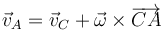
\vec{v}_A = \vec{v}_C + \vec{\omega}\times\overrightarrow{CA}

Tomando un sistema de ejes en el que X es en la dirección de avance paralela al plano, Y es ortogonal a éste y Z el eje perpendicular a ambos (perpendicular al plano de movimiento y hacia afura del papel o pantalla), estos vectores se pueden escribir

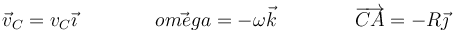
\vec{v}_C = v_C\vec{\imath}\qquad\qquad \vec{omega}=-\omega\vec{k}\qquad\qquad \overrightarrow{CA}=-R\vec{\jmath}

El signo negativo de la velocidad angular es porque por simple intuición sabemos que gira en sentido horario (negativo) respecto al eje Z, pero el problema se puede resolver igualmente sin suponer este signo. Sustituyendo nos queda

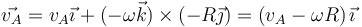
\vec{v_A}=v_A\vec{\imath}+(-\omega\vec{k})\times(-R\vec{\jmath})=\left(v_A-\omega R\right)\vec{\imath}

pero puesto que el cilindro rueda sin deslizar la velocidad del punto de contacto es nula.

v_A\qquad\Rightarrow\qquad v_C = \omega R

Puesto que esta relación se cumple en todo instante, podemos derivarla respecto al tiempo y obtener

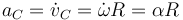
a_C = \dot{v}_C = \dot{\omega}R = \alpha R

Por tanto, tenemos la relación entre las aceleraciones

a_c = \alpha R\qquad\qquad\mbox{pero}\qquad\qquad \vec{a}_C \neq \vec{\alpha}R

La relación de proporcionalidad es entre módulos, no entre vectores, pues apuntan en direcciones diferentes

\vec{a}_C = a_C\vec{\imath}\qquad\qquad \vec{\alpha}=-\frac{a_C}{R}\vec{k}

3 Aceleración del CM

El valor de la aceleración lo podemos obtener a partir de las fuerzas o mediante razonamientos energéticos.

3.1 A partir de las fuerzas

Las leyes de la dinámica para un sólido nos dan la ecuación

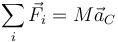
\sum_i\vec{F}_i = M\vec{a}_C

siendo las fuerzas que se aplican sobre el cilindro

  • El peso
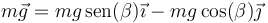
m\vec{g}=mg\,\mathrm{sen}(\beta)\vec{\imath}-mg\cos(\beta)\vec{\jmath}
  • La fuerza normal
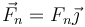
\vec{F}_n = F_n\vec{\jmath}
  • La fuerza de rozamiento
\vec{F}_r = -F_r\vec{\imath}

lo que llevado a la segunda ley de Newton y separado en componentes nos da las relaciones

\left\{\begin{array}{rcl} ma_c & = & mg\,\mathrm{sen}(\beta)-F_r \\ 0 & = & -mg\cos(\beta)+F_n\end{array}\right.

4 Condición sobre el rozamiento

Obtenido de "http://tesla.us.es/wiki/index.php/Cilindro_que_rueda_por_una_pendiente"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace