Fuerza magnética entre dos hilos paralelos

De Laplace

(Diferencias entre revisiones)

Revisión de 14:52 20 jun 2013

1 Enunciado

Se tienen dos hilos paralelos, de longitud indefinida, separados una distancia $a$ . Calcule la fuerza magnética sobre una porción de longitud $h$ de uno de los hilos debida al otro cuando por ellos circulan corrientes $I 1$ e $I 2$ .

2 Solución

Este problema es una extensión bastante simple del cálculo de la fuerza entre dos cargas en movimiento paralelo.

Suponemos el eje Z sobre uno de los hilos. Si por este hilo circula una corriente $I 1$ , el campo magnético que produce es

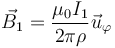
$\vec{B}_1 = \frac{\mu_0I_1}{2\pi\rho}\vec{u}_\varphi$

Si ahora consideramos que el segundo hilo está situado paralelamente al eje Z y sobre el punto $x = a$ , $y = 0$ , para todos los puntos el segundo hilo

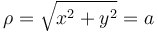
$\rho = \sqrt{x^2+y^2}=a$

mientras que el vector 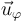$\vec{u}_\varphi$ en todos los puntos del segundo hilo es

$\vec{u}_\phi(x=a,y=0) = \vec{\jmath}$

por lo que el campo magnético del primer hilo en los puntos del segundo se puede escribir

$\vec{B}_1(x=a,y=0)= \frac{\mu_0I_1}{2\pi a}\vec{\jmath}$

La fuerza sobre un tramo del segundo hilo la da la integral

$\vec{F}_{1\to 2}=I_2\int_A^B \mathrm{d}\vec{r}_2\times\vec{B}_1(\vec{r}_2)$

que en este caso, aplicando que

$\vec{r}_2 = z\vec{k}\qquad\qquad\mathrm{d}\vec{r}_2=\mathrm{d}z\,\vec{k}\qquad \qquad z\in[0,h]$

se reduce a

No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \vec{F}_{1\to 2}=I_2\int_0^h \mathrm{d}z\vec{k}\times\left(\frac{\mu_0I_1}{2\pi a}vec{\jmath}\right) \=-\frac{\mu_0I_1I_2}{2\pi a}\vec{\imath}

@@ Línea 25: / Línea 25: @@
 <center><math>\vec{F}_{1\to 2}=I_2\int_A^B \mathrm{d}\vec{r}_2\times\vec{B}_1(\vec{r}_2)</math></center>
-que en este caso se reduce a
+que en este caso, aplicando que
 <center><math>\vec{r}_2 = z\vec{k}\qquad\qquad\mathrm{d}\vec{r}_2=\mathrm{d}z\,\vec{k}\qquad \qquad z\in[0,h]</math></center>
-<center><math>\vec{F}_{1\to 2}=I_2\int_0^h \mathrm{d}z\vec{k}\times\left(\frac{\mu_0I_1}{2\pi a}\right) \vec{\jmath}=-\frac{\mu_0I_1I_2}{2\pi a}\vec{\imath}</math></center>
+se reduce a
+<center><math>\vec{F}_{1\to 2}=I_2\int_0^h \mathrm{d}z\vec{k}\times\left(\frac{\mu_0I_1}{2\pi a}vec{\jmath}\right) \=-\frac{\mu_0I_1I_2}{2\pi a}\vec{\imath}</math></center>
 [[Categoría:Problemas de campo magnético (GIE)]]

Fuerza magnética entre dos hilos paralelos

De Laplace

Revisión de 14:52 20 jun 2013

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES