Conexiones de cuatro bombillas
De Laplace
(→Resistencia de cada bombilla) |
|||
| Línea 24: | Línea 24: | ||
R_D & = & \displaystyle\frac{120^2 \mathrm{V}^2}{40\,\mathrm{W}}= 360\,\Omega \end{array}</math></center> | R_D & = & \displaystyle\frac{120^2 \mathrm{V}^2}{40\,\mathrm{W}}= 360\,\Omega \end{array}</math></center> | ||
| + | A partir de aquí podemos olvidarnos de las potencias nominales y trabajar exclusivamente con las resistencias. | ||
==Antes de cerrar el interruptor== | ==Antes de cerrar el interruptor== | ||
| + | Inicialmente tenemos un circuito formado por dos ramas en paralelo, cada una de las cuales consta de dos resistencias puestas en serie. | ||
| + | |||
| + | Al estar en paralelo, la diferencia de potencial en la rama superior es la misma que en la inferior e igual a la aplicada por la fuente, que es de 120V. Para cada una de las ramas se aplica lo que se demuestra en otro [[Asociación_de_dos_bombillas_en_serie|problema]]. | ||
| + | |||
| + | Considerando primero la rama superior tenemos dos resistencias en serie, por las cuales circula la misma intensidad de corriente. La potencia disipada en cada una es | ||
| + | |||
| + | <center><math>P_A = I_1^2 R_A\qquad\qquad P_B = I_1^2 R_B</math></center> | ||
| + | |||
| + | siendo la corriente que circula por esta rama | ||
| + | |||
| + | <center><math>I_1 = \frac{\Delta V}{R_A+R_B} = \frac{120\,\mathrm{V}}{(480+240)\,\Omega}=\frac{1}{6}\,\mathrm{A}=0.167\,\mathrm{A}</math></center> | ||
| + | |||
| + | con lo que obtenemos las potencias | ||
| + | |||
| + | <center><math>P_A = (\frac{1}{6})^2\times 480\,\mathrm{W} = \frac{40}{3}\,\mathrm{W}=13.3\,\mathrm{W}\qquad\qquad P_B = \left(\frac{1}{6}\right)^2\times 240\,\mathrm{W}=\frac{20}{3}\mathrm{W}=6.67\,\mathrm{W}</math></center> | ||
==Después de cerrar el interruptor== | ==Después de cerrar el interruptor== | ||
[[Categoría:Problemas de corriente eléctrica (GIE)]] | [[Categoría:Problemas de corriente eléctrica (GIE)]] | ||
Revisión de 22:38 18 jun 2013
Contenido |
1 Enunciado
Se dispone de cuatro bombillas, A, B, C, D. El etiquetado de estas bombillas indica que, para un voltaje de 120V, sus potencias nominales son respectivamente 30W, 60W, 120W y 40W. Se montas la cuatro bombillas en el siguiente esquema y se aplica entre los extremos una diferencia de potencial de 120V.
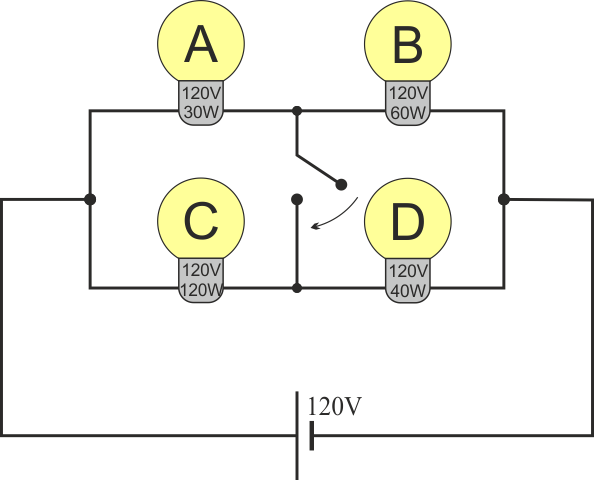
- Calcule el consumo de cada bombilla (en vatios) para este montaje, así como el consumo total del montaje. ¿Cuál es la que da más luz? ¿Y la que menos?
- Suponga que se cierra el interruptor central. Una vez cerrado, ¿cuál es el nuevo consumo total y el individual? ¿Cuál es ahora la bombilla más brillante y la menos brillante?
2 Resistencia de cada bombilla
Este problema se reduce a calcular las potencias disipadas en una serie de resistencias. Para resolverlo, primero debemos calcular los valores de éstas, empleando las potencias nominales.
Cuando en un aparato eléctrico (una bombilla, una plancha, una estufa) sus especificaciones indican valores como 120V 40W, queiere decir que si aplica una diferencia de potencial de 120V entre sus terminales, la potencia que consume es de 40W. Puesto que la potencia consumida en una resistencia por efecto Joule verifica
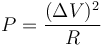
obtenemos la resistencia de cada bombilla como
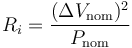
esto nos da, para las cuatro0 bombillas
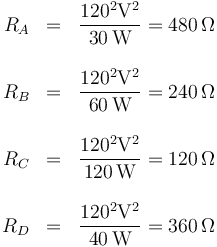
A partir de aquí podemos olvidarnos de las potencias nominales y trabajar exclusivamente con las resistencias.
3 Antes de cerrar el interruptor
Inicialmente tenemos un circuito formado por dos ramas en paralelo, cada una de las cuales consta de dos resistencias puestas en serie.
Al estar en paralelo, la diferencia de potencial en la rama superior es la misma que en la inferior e igual a la aplicada por la fuente, que es de 120V. Para cada una de las ramas se aplica lo que se demuestra en otro problema.
Considerando primero la rama superior tenemos dos resistencias en serie, por las cuales circula la misma intensidad de corriente. La potencia disipada en cada una es

siendo la corriente que circula por esta rama
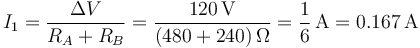
con lo que obtenemos las potencias






