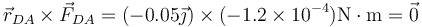Entrar Página Discusión Historial Go to the site toolbox

Fuerza magnética sobre una espira inclinada

De Laplace

(Diferencias entre revisiones)
(→Par)
Línea 58: Línea 58:
;Lado AB:
;Lado AB:
-
<center><math>\vec{r}_{AB}=\frac{\vec{r}_A+\vec{r}_B}{2}=(3\vec{\imath}-4\vec{k})\,\mathrm{cm}</math>{{qquad}}{{qquad}}<math>\vec{r}_{AB}\times\vec{F}_{AB}=(0.03\vec{\imath}-0.04\times\vec{k})\times (0.01\vec{k})\mathrm{N\cdot m}=-0.08\vec{\jmath}\mathrm{N\cdot m}</math></center>
+
<center><math>\vec{r}_{AB}=\frac{\vec{r}_A+\vec{r}_B}{2}=(3\vec{\imath}-4\vec{k})\,\mathrm{cm}</math>{{qquad}}{{qquad}}<math>\vec{r}_{AB}\times\vec{F}_{AB}=(0.03\vec{\imath}-0.04\vec{k})\times (2\times^{-4}\vec{k})\mathrm{N\cdot m}=-8\vec{\jmath}\,\mu\mathrm{N}\cdot\mathrm{m}</math></center>
 +
 
 +
;Lado BC:
 +
 
 +
<center><math>\vec{r}_{BC}=\frac{\vec{r}_B+\vec{r}_C}{2}=(5\vec{\jmath})\,\mathrm{cm}</math>{{qquad}}{{qquad}}<math>\vec{r}_{BC}\times\vec{F}_{BC}=(0.05\vec{\jmath})\times (1.2\times 10^{-4})\mathrm{N\cdot m}=\vec{0}</math></center>
 +
 
 +
;Lado CD:
 +
 
 +
<center><math>\vec{r}_{CD}\times\vec{F}_{AB}=(-0.03\vec{\imath}+0.04\vec{k})\times (-2\times^{-4}\vec{k})\mathrm{N\cdot m}=-8\vec{\jmath}\,\mu\mathrm{N}\cdot\mathrm{m}</math></center>
 +
 
 +
;Lado DA:
 +
 
 +
<center><math>\vec{r}_{DA}\times\vec{F}_{DA}=(-0.05\vec{\jmath})\times (-1.2\times 10^{-4})\mathrm{N\cdot m}=\vec{0}</math></center>
 +
 
==Momento magnético==
==Momento magnético==
[[Categoría:Problemas de campo magnético (GIE)]]
[[Categoría:Problemas de campo magnético (GIE)]]

Revisión de 21:06 12 jun 2013

Contenido

1 Enunciado

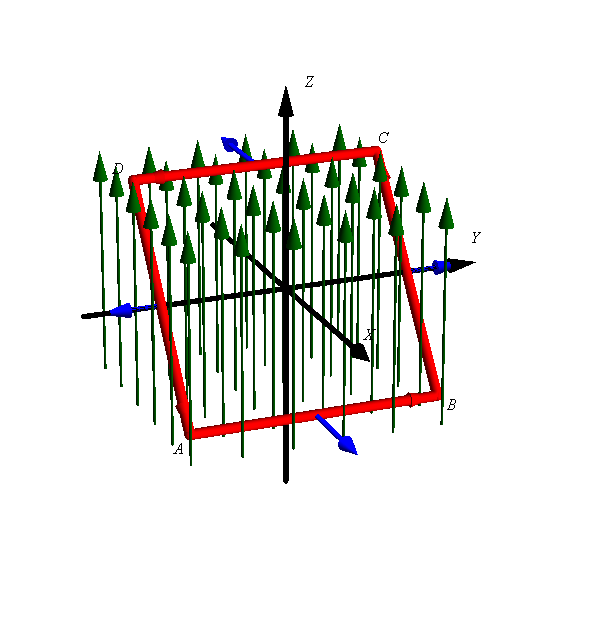
Una espira cuadrada ABCD de lado 10 cm se encuentra en el interior de un campo magnético uniforme 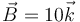\vec{B}=10\vec{k} (mT). Los vértices de la espira se encuentran en

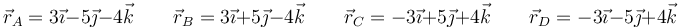
\vec{r}_A=3\vec{\imath}-5\vec{\jmath}-4\vec{k}\qquad \vec{r}_B=3\vec{\imath}+5\vec{\jmath}-4\vec{k}\qquad \vec{r}_C=-3\vec{\imath}+5\vec{\jmath}+4\vec{k}\qquad \vec{r}_D=-3\vec{\imath}-5\vec{\jmath}+4\vec{k}

(distancias medidas en cm). Por la espira circula una corriente de 0.2 A en el sentido ABCD.

  1. Halle la fuerza magnética sobre cada lado de la espira, así como la fuerza total sobre la espira
  2. Considerando cada fuerza aplicada sobre el centro del lado correspondiente, halle el momento resultante, según la ley
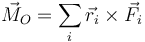
\vec{M}_O=\sum_i\vec{r}_i\times\vec{F}_i
  1. Calcule el momento magnético de la espira y compruebe que
\vec{M}_O = \vec{m}\times\vec{B}\qquad\qquad (\vec{m}=IS\vec{n})

2 Fuerzas

La fuerza sobre un segmento rectilíneo por el cual circula una intensidad de corriente I, inmerso en un campo magnético uniforme vale

\vec{F}_{AB} = I(\Delta \vec{r})\times\vec{B}\qquad\qquad \Delta\vec{r}=\overrightarrow{AB}=\vec{r}_B-\vec{r}_{A}

que aplicado a cada caso nos da

Lado AB
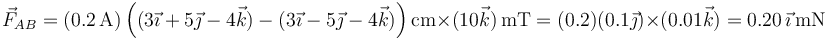
\vec{F}_{AB}=(0.2\,\mathrm{A})\left((3\vec{\imath}+5\vec{\jmath}-4\vec{k})-(3\vec{\imath}-5\vec{\jmath}-4\vec{k})\right)\mathrm{cm}\times(10\vec{k})\,\mathrm{mT}=(0.2)(0.1\vec{\jmath})\times(0.01\vec{k})=0.20\,\vec{\imath}\,\mathrm{mN}
Lado BC
\vec{F}_{BC}=(0.2\,\mathrm{A})\left((-3\vec{\imath}+5\vec{\jmath}+4\vec{k})-(3\vec{\imath}+5\vec{\jmath}-4\vec{k})\right)\mathrm{cm}\times(10\vec{k})\,\mathrm{mT}=(0.2)(-0.06\vec{\imath}+0.08\vec{k})\times(0.01\vec{k})=0.12\,\vec{\jmath}\,\mathrm{mN}
Lado CD
\vec{F}_{CD}=-0.20\,\vec{\imath}\,\mathrm{mN}
Lado DA
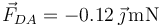
\vec{F}_{DA}=-0.12\,\vec{\jmath}\,\mathrm{mN}

Siendo la fuerza total sobre la espira

\vec{F}=\vec{F}_{AB}+\vec{F}_{BC}+\vec{F}_{CD}+\vec{F}_{DA}=\vec{0}
Archivo:fuerza-espira.png

3 Par

El que la resultante de las fuerzas se anula no quiere decir que el campo magnético no ejerza fuerza alguna sobre la espira. Solo implica que su centro de masas no se acelera.

Al estar las fuerzas aplicadas sobre a lo largo de rectas paralelas, lo que sí se produce es un par de fuerzas. La fuerza sobre el lado superior de la espira y la fuerza sobre el lado inferior tienden a producir un giro de ésta alrededor del eje OX.

Para medir este efecto calculamos la resultante del momento de las fuerzas aplicadas

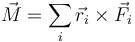
\vec{M}=\sum_i \vec{r}_i\times \vec{F}_i

siendo el punto de aplicación de cada una el punto medio de cada lado. Así tenemos

Lado AB
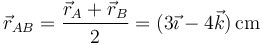
\vec{r}_{AB}=\frac{\vec{r}_A+\vec{r}_B}{2}=(3\vec{\imath}-4\vec{k})\,\mathrm{cm}        \vec{r}_{AB}\times\vec{F}_{AB}=(0.03\vec{\imath}-0.04\vec{k})\times (2\times^{-4}\vec{k})\mathrm{N\cdot m}=-8\vec{\jmath}\,\mu\mathrm{N}\cdot\mathrm{m}
Lado BC
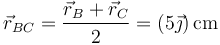
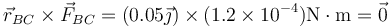
\vec{r}_{BC}=\frac{\vec{r}_B+\vec{r}_C}{2}=(5\vec{\jmath})\,\mathrm{cm}        \vec{r}_{BC}\times\vec{F}_{BC}=(0.05\vec{\jmath})\times (1.2\times 10^{-4})\mathrm{N\cdot m}=\vec{0}
Lado CD
\vec{r}_{CD}\times\vec{F}_{AB}=(-0.03\vec{\imath}+0.04\vec{k})\times (-2\times^{-4}\vec{k})\mathrm{N\cdot m}=-8\vec{\jmath}\,\mu\mathrm{N}\cdot\mathrm{m}
Lado DA
\vec{r}_{DA}\times\vec{F}_{DA}=(-0.05\vec{\jmath})\times (-1.2\times 10^{-4})\mathrm{N\cdot m}=\vec{0}

4 Momento magnético

Obtenido de "http://tesla.us.es/wiki/index.php/Fuerza_magn%C3%A9tica_sobre_una_espira_inclinada"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace