Coeficientes de inducción mutua y autoinducción (GIE)
De Laplace
(→Ley de Faraday) |
(→Ley de Faraday) |
||
| Línea 65: | Línea 65: | ||
Si en lugar de una espira tenemos <math>N</math> espiras, rígidas y en una posición relativa fija, la f.e.m. que se induce en la espira <math>i</math> tendrá contribuciones de cada una de las espiras | Si en lugar de una espira tenemos <math>N</math> espiras, rígidas y en una posición relativa fija, la f.e.m. que se induce en la espira <math>i</math> tendrá contribuciones de cada una de las espiras | ||
| - | <center><math>\mathcal{E}_i = -\sum_k L_{ik}\ | + | <center><math>\mathcal{E}_i = -\sum_k L_{ik}\frac{\mathrm{d}I_k}{\mathrm{d}t}</math></center> |
Esta fuerza electromotriz inducida habrá que añadirla a otras posibles fuentes, como generadores de tensión. | Esta fuerza electromotriz inducida habrá que añadirla a otras posibles fuentes, como generadores de tensión. | ||
[[Categoría:Inducción electromagnética (GIE)]] | [[Categoría:Inducción electromagnética (GIE)]] | ||
Revisión de 12:02 24 may 2013
Contenido |
1 Flujo magnético
Uno de los principios básicos del magnetismo (expresado mediante la ley de Biot y Savart) es que una corriente eléctrica que circula por un circuito produce un campo magnético. En la mayoría de las situaciones, el campo magnético producido es proporcional a la intensidad corriente que lo produce.
El campo magnético verifica asimismo el principio de superposición: si tenemos diferentes corrientes, el campo total es la suma del que produce cada corriente por separado.
Dada una curva cerrada Γ, se denomina flujo magnético a la cantidad
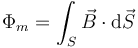
siendo S una superficie abierta apoyada en Γ.
1.1 Autoinducción
Si tenemos una espira cerrada, por la cual circula una corriente I, el flujo magnético a través de una superficie apoyada en la propia espira, será proporcional a la corriente que circula por ella
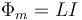
siendo L el denominado coeficiente de autoinducción, cuya unidad es el Henrio (H)
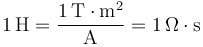
1.2 Inducción mutua=
Si en lugar de una sola espira tenemos un conjunto de ellas, por las cuales circulan corrientes Ik, el flujo a través de una superficie Si apoyada en la espira i tendrá una contribución por cada una de las espiras
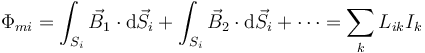
Las cantidades Lik para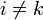 
se denominan coeficientes de inducción mutua. Se miden asimismo en Henrios. Para i = k tenemos los coeficientes de autoinducción (del cual el sistema de una sola espira es un caso particular).
Los coeficientes de inducción mutua forman una matriz simétrica
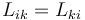
en la que los términos diagonales son siempre estrictamente positivos, mientras que los no diagonales pueden tener cualquier signo o ser nulos.
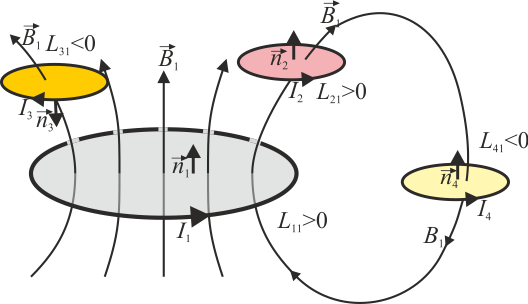
Para conocer el signo de cada coeficiente debe aplicarse el criterio siguiente:
- Para cada espira Γi se asigna un sentido de recorrido de la corriente.
- La regla de la mano derecha establece el sentido de la normal
a la superficie Si apoyada en Γi.
- El campo magnético producido por la espira Γk verifica asimismo la regla de la mano derecha respecto de la corriente que lo produce.
- El flujo del campo magnético es positivo si
y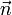 
van el mismo sentido y negativo en caso contrario.
- Por tanto, si el campo
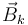entra en la espira i según la orientación dada por la regla de la mano derecha para esta espira, Lik > 0. En caso contrario Lik < 0.
- Como caso particular, los coeficientes de autoinducción Lkk, son siempre positivos.
2 Ley de Faraday
La inducción electromagnética se basa en que, a lo largo de una espira Γ, atravesada por un campo magnético cuyo flujo es variable en el tiempo, se induce una fuerza electromotriz (f.e.m.) dada por
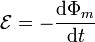
Esta es la llamada ley de Faraday. Si tenemos una espira cerrada Γ, rígida, por la cual circula una corriente variable I(t), esta corriente, por la ley de Biot y Savart, producirá un campo magnético proporcional a ella. El flujo de este campo también variará en el tiempo, y por tanto inducirá una fuerza electromotriz, según la ley de Faraday
La condición de rigidez es necesaria para poder extraer L de la derivada.
Si en lugar de una espira tenemos N espiras, rígidas y en una posición relativa fija, la f.e.m. que se induce en la espira i tendrá contribuciones de cada una de las espiras
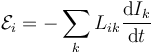
Esta fuerza electromotriz inducida habrá que añadirla a otras posibles fuentes, como generadores de tensión.
