Principios de la electrostática (GIE)
De Laplace
(→Ley de Coulomb) |
(→Campo eléctrico) |
||
| Línea 83: | Línea 83: | ||
==Principio de superposición== | ==Principio de superposición== | ||
==Campo eléctrico== | ==Campo eléctrico== | ||
| + | Entendemos el campo eléctrostático como una perturbación en el espacio producida por la presencia de cargas eléctricas en reposo | ||
| + | |||
| + | {| class="bordeado" | ||
| + | |- | ||
| + | | [[Archivo:campo-carga-positiva.png]] | ||
| + | | [[Archivo:campo-carga-negativa.png]] | ||
| + | |- | ||
| + | | [[Archivo:campo-dipolo-electrico.png]] | ||
| + | | [[Archivo:campo-cuatro-cargas.png]] | ||
| + | |} | ||
| + | |||
| + | (ilustraciones obra de [http://commons.wikimedia.org/wiki/User:Geek3 Geek3] para Wikipedia). | ||
| + | |||
| + | El campo es un concepto primario. No se puede describir qué es el campo eléctrico, sino solo qué efectos produce sobre otras cargas. | ||
| + | |||
| + | Puede definirse de una manera operativa, esto es, dando un procedimiento para su medida. Para ello se considera una carga muy pequeña <math>q_0</math> y se sitúa en un campo eléctrico. Con la medida de un dinamómetro se mide la fuerza sobre ella. Se define el campo eléctrico en la posición de la carga como | ||
| + | |||
| + | <center><math>\vec{E}(\vec{r})=\lim_{q_0\to 0}\frac{\vec{F}}{q_0}</math></center> | ||
| + | |||
| + | El límite se toma porque idealmente se considera que la carga que se coloca no debe afectar a lo que ya había, para lo cual debe ser lo más pequeña posible. | ||
| + | |||
| + | ==Líneas de campo eléctrico== | ||
| + | Como con cualquier otro campo, se pueden trazar las líneas de campo eléctrico, como aquellas curvas que son tangentes al campo eléctrico en cada punto. Estas curvas son soluciones de la ecuación diferencial | ||
| + | |||
| + | <center><math>\mathrm{d}\vec{r}=\vec{E}(\vec{r})\,\mathrm{d}\theta\qquad\Rightarrow\qquad \frac{\mathrm{d}\vec{r}}{\mathrm{d}\theta}=\vec{E}(\vec{r})</math></center> | ||
| + | |||
| + | siendo <math>\theta</math> un parámetro que nos permite etiquetar los puntos de cada curva. Estas ecuaciones diferenciales suelen ser extremadamente complejas y no poseen soluciones analíticas salvo en los casos más triviales, por lo que su solución requiere el uso de ordenadores, como en el caso de las cuatro cargas representado más arriba. | ||
| + | |||
| + | Existe casos particulares importantes: | ||
| + | |||
| + | * Un campo uniforme (independiente de la posición) tiene líneas de campo que son rectas paralelas. Este es el caso del campo eléctrico en el interior de un condensador plano. | ||
| + | |||
| + | <center>[[Archivo:campo-interior-condensador.png|300px]]</center> | ||
| + | * Un campo central | ||
| + | |||
| + | <center><math>\vec{E}(\vec{r}) = E(r)\vec{u}_r\qquad \qquad (\mbox{campo central})</math></center> | ||
| + | |||
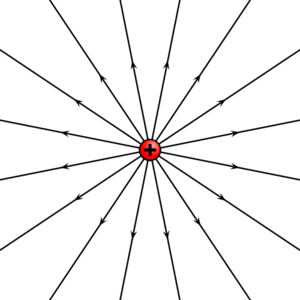
| + | :en el cual el campo es siempre puramente radial, las líneas de campo son semirrectas radiales. Este es el caso del campo de una carga puntual, positiva o negativa, | ||
| + | |||
| + | {| class="bordeado" | ||
| + | |- | ||
| + | | [[Archivo:campo-carga-positiva.png|300px]] | ||
| + | | [[Archivo:campo-carga-negativa.png|300px]] | ||
| + | |- | ||
| + | |} | ||
| + | |||
[[Categoría:Electrostática en el vacío (GIE)]] | [[Categoría:Electrostática en el vacío (GIE)]] | ||
Revisión de 12:42 9 abr 2013
Contenido |
1 Concepto de electrostática
La Electrostática es la parte del electromagnetismo que estudia la interacción entre cargas eléctricas en reposo.
Por estar cargadas y a una cierta distancia, las partículas ejercen fuerzas eléctricas unas sobre otras. De acuerdo con la segunda Ley de Newton, el resultado de estas fuerzas debe ser un movimiento acelerado de las diferentes cargas. Supondremos que esto no ocurre porque actúan sobre ellas otras fuerzas no consideradas que retienen a las cargas en la misma posición.
A pesar de su aparente irrealidad (ya que una carga no puede mantenerse inmóvil flotando en el espacio), la electrostática posee una gran aplicación ya que no solo describe aproximadamente situaciones reales, sino porque sirve de fundamento para otras situaciones electromagnéticas. En el campo de la electrostática aparecen el principio de superposición, la ley de Gauss, el potencial eléctrico, la ecuación de Laplace… todos los cuales se utilizan más adelante.
La electrostática se subdivide en dos situaciones:
- Electrostática en el vacío
- Supone que las cargas están inmóviles flotando en el espacio.
- Electrostática en medios materiales
- Supone que las cargas se encuentran en el interior o en la superficie de medios materiales. A su vez, éstos se suelen clasificar en dos tipos:
- Conductores
- Son aquellos materiales (típicamente metálicos) que permiten el movimiento de cargas por su interior. En electrostática esto implica que las cargas se encuentran en equilibrio ya que pudiendo moverse no lo hacen.
- Dieléctricos
- Son aquellos materiales (típicamente plásticos) que no permiten el movimiento de cargas por su interior. En electrostática esto implica la existencia de cargas ligadas, que no pueden abandonar los átomos a los que pertenecen.
Aunque en la mayoría de los casos prácticos consideraremos cargas dentro de medios materiales, la electrostática en el vacío es válida como fundamento de todo lo que sigue, puesto que estos son vacío en su mayor parte.
2 Ley de Coulomb
La ley de Coulomb fue descubierta por Henry Cavendish, que no lo publicó. Varios años después, Coulomb redescubrió esta ley, publicándolo adecuadamente, por lo que recibe su nombre.
Es una ley física que nos describe la fuerza entre dos cargas puntuales en reposo. Nos dice que si tenemos dos cargas puntuales q1 y q2 situadas a una distancia d12, aparece una fuerza eléctrica entre ellas tal que:
- Módulo
- es proporcional al producto de las cargas.
- es inversamente proporcional al cuadrado de la distancia entre las cargas.
- Dirección
- Es la de la recta que pasa por las dos cargas
- Sentido
- Depende del signo de las cargas
- Cargas del mismo signo se repelen
- Cargas de distinto signo se atraen
Matemáticamente esto se expresa como que la fuerza que produce la carga 1 sobre la 2 es
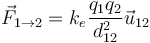
siendo 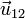 el vector unitario en la dirección de la recta que pasa por las dos cargas y lleva el sentido de la 1 a la 2, es decir, hacia fuera de las dos cargas. La fuerza que la 2 produce sobre la 1 se calculará del mismo modo, sustituyendo
el vector unitario en la dirección de la recta que pasa por las dos cargas y lleva el sentido de la 1 a la 2, es decir, hacia fuera de las dos cargas. La fuerza que la 2 produce sobre la 1 se calculará del mismo modo, sustituyendo 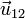 por
por 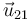 que es el unitario opuesto.
que es el unitario opuesto.
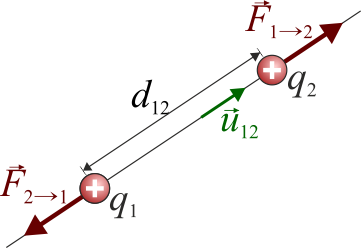
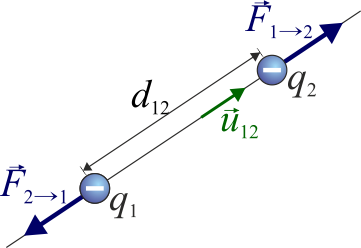
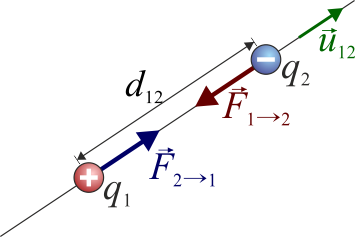
Esta expresión es válida tanto si las cargas son del mismo signo como si son de signos opuestos. En el segundo caso, el producto de las cargas es negativo y resulta una fuerza atractiva.
La constante ke universal que, por la forma en que se eligen las unidades en el SI tiene un valor exacto
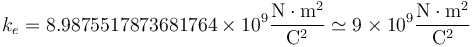
siendo el segundo valor mucho más fácil de recorrar y con un error de solo el 0.1%.
Esta constante de proporcionalidad suele escribirse en la forma aparentemente más complicada
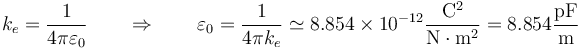
La razón de escribirlo de esta forma se halla en la ley de Gauss.
Si lo que conocemos son los vectores de posición de las dos cargas respecto a un sistema de referencia, podemos escribir la ley de Coulomb en función de estos vectores, ya que

y queda
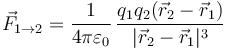
Hay que destacar (porque es fuente de errores) el cambio del exponente del denominador de 2 a 3, al introducir una distancia más en la normalización del vector de posición relativo.
Como ilustración de la magnitud la fuerza eléctrica podemos considerar la atracción entre un protón y un electrón que se hallan a una distancia de un radio de Bohr (tamaño del átomo de hidrógeno)
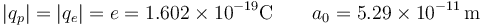
Resulta un módulo de la fuerza
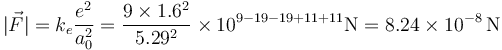
Esta fuerza no parece excesivamente intensa, pero debemos tener en cuenta que actúa sobre un electrón, cuya masa es minúscula. La aceleración que produce esta fuerza es

Dicho de otra forma, la fuerza debida a un solo protón es 9000000000000000000000 veces la atracción gravitatoria debida a la Tierra entera.
Otra comparación posible es la de la fuerza eléctrica entre el protón y el electrón y la fuerza gravitatoria entre ellas. Su cociente vale
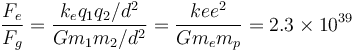
es decir, la fuerza eléctrica es 2300000000000000000000000000000000000000 veces más intensa que la gravitatoria.
3 Principio de superposición
4 Campo eléctrico
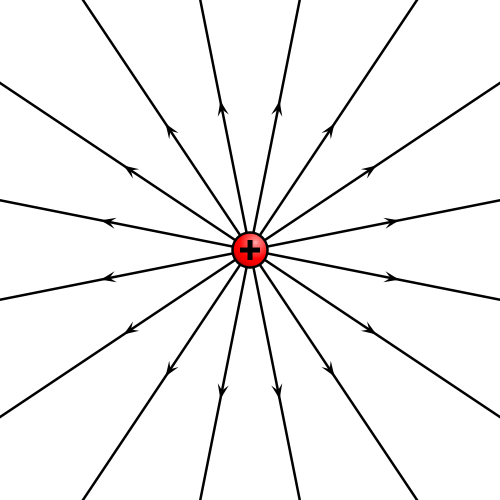
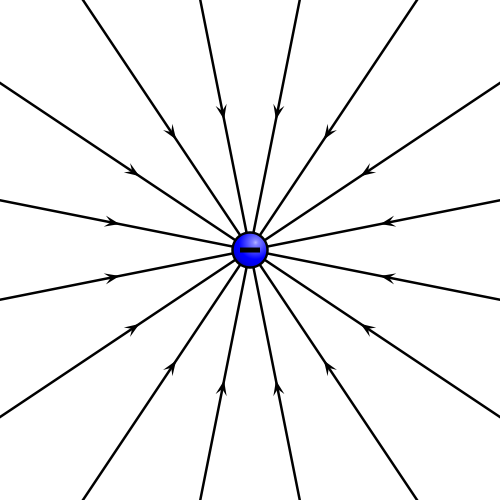
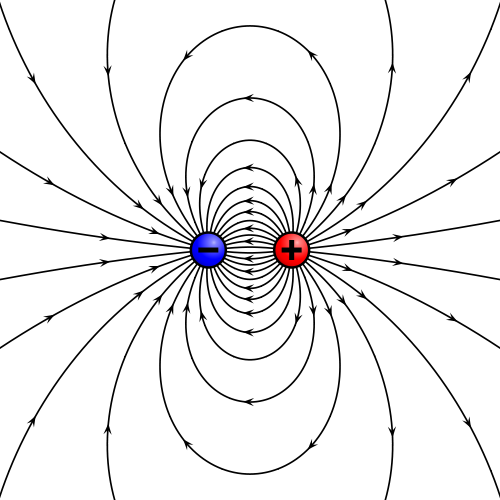
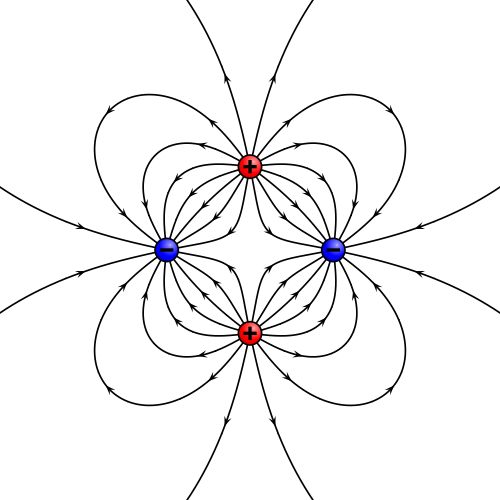
Entendemos el campo eléctrostático como una perturbación en el espacio producida por la presencia de cargas eléctricas en reposo
| 
|
| 
|
(ilustraciones obra de Geek3 para Wikipedia).
El campo es un concepto primario. No se puede describir qué es el campo eléctrico, sino solo qué efectos produce sobre otras cargas.
Puede definirse de una manera operativa, esto es, dando un procedimiento para su medida. Para ello se considera una carga muy pequeña q0 y se sitúa en un campo eléctrico. Con la medida de un dinamómetro se mide la fuerza sobre ella. Se define el campo eléctrico en la posición de la carga como
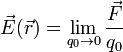
El límite se toma porque idealmente se considera que la carga que se coloca no debe afectar a lo que ya había, para lo cual debe ser lo más pequeña posible.
5 Líneas de campo eléctrico
Como con cualquier otro campo, se pueden trazar las líneas de campo eléctrico, como aquellas curvas que son tangentes al campo eléctrico en cada punto. Estas curvas son soluciones de la ecuación diferencial
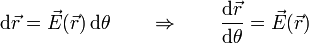
siendo θ un parámetro que nos permite etiquetar los puntos de cada curva. Estas ecuaciones diferenciales suelen ser extremadamente complejas y no poseen soluciones analíticas salvo en los casos más triviales, por lo que su solución requiere el uso de ordenadores, como en el caso de las cuatro cargas representado más arriba.
Existe casos particulares importantes:
- Un campo uniforme (independiente de la posición) tiene líneas de campo que son rectas paralelas. Este es el caso del campo eléctrico en el interior de un condensador plano.
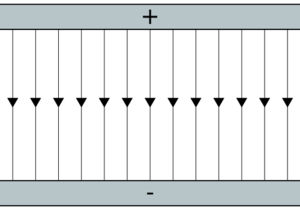
- Un campo central

- en el cual el campo es siempre puramente radial, las líneas de campo son semirrectas radiales. Este es el caso del campo de una carga puntual, positiva o negativa,
| 
|





