Caso de ciclo Ericsson
De Laplace
(→Representación gráfica) |
(→A→B) |
||
| Línea 44: | Línea 44: | ||
El volumen de este estado B lo hallamos aplicando la ley de Boyle (caso particular de la ley de los gases ideales) | El volumen de este estado B lo hallamos aplicando la ley de Boyle (caso particular de la ley de los gases ideales) | ||
| - | <center><math>V_B=\frac{p_AV_A}{p_B}=\frac{1.0\,\mathrm{bar}\times 160\,\mathrm{cm}^3}{1.25 | + | <center><math>V_B=\frac{p_AV_A}{p_B}=\frac{1.0\,\mathrm{bar}\times 160\,\mathrm{cm}^3}{1.25\,\mathrm{bar}}=128\,\mathrm{bar}=1.28\times 10^{-4}\mathrm{m}^3</math></center> |
Esto quiere decir que la nueva altura del pistón es | Esto quiere decir que la nueva altura del pistón es | ||
Revisión de 10:30 14 mar 2013
Contenido |
1 Enunciado
Se tiene un cilindro vertical de paredes no aislantes, en cuyo interior se encuentra aire (considerado como un gas ideal diatómico). El cilindro tiene sección cuadrada de lado 4 cm y está cerrado por un pistón horizontal que puede deslizarse sin rozamiento.
Inicialmente el pistón se encuentra a una altura de 10 cm y el aire está en equilibrio térmico y mecánico con el exterior a una temperatura de 300 K y una presión 100 kPa.
Se procede entonces a efectuar el siguiente ciclo
- A→B El gas se comprime lentamente, colocando sobre la tapa el equivalente a 4 kg de arena, sin que se modifique la temperatura exterior.
- B→C Sin retirar la arena, se calienta lentamente el gas, hasta que el volumen vuelve a ser el inicial.
- C→D Manteniendo constante la nueva temperatura, se van retirando los granos de arena hasta que no queda ni uno.
- D→A Se enfría gradualmente el gas, hasta que su volumen vuelve a ser el inicial.
A la vista de este ciclo:
- Represente gráficamente el ciclo en un diagrama pV.
- Para cada uno de los pasos, halle (tomando
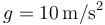 )
)
- El trabajo y el calor que se intercambian, indicando si cada uno entra en el sistema o sale de él.
- La variación de la energía interna y de la entalpía del gas en cada paso.
- Calcule el trabajo neto que desarrolla el sistema sobre el entorno.
- Halle el calor total absorbido por el gas (sin descontar el que cede al entorno).
- Calcule el rendimiento del ciclo, definido como:
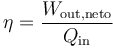
2 Representación gráfica
Aunque es fácil hacer una representación gráfica esquemática, vamos a construir una exacta empleando los valores de los diferentes estados del ciclo, así como las curvas que los unen.
2.1 A→B
En el primer paso tenemos que se va aumentando lentamente la presión sobre el gas, manteniéndose constante la temperatura. El proceso es una compresión isoterma, que podemos suponer cuasiestática. En todo momento se cumple la ley de Boyle
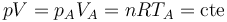
Gráficamente, el proceso se representa por un arco de hipérbola. El estado inicial corresponde a una presión y un volumen
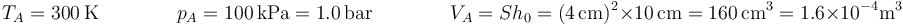
El estado final B tiene la misma temperatura, mientras que su presión aumenta en la cantidad correspondiente al peso añadido
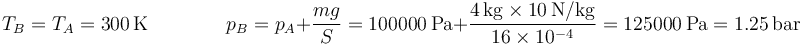
Este resultado no es muy exacto porque hemos tomado g = 10m/s² en vez de g = 9.8m/s², pero por una mayor simplicidad en los cálculos, lo mantendremos así.
El volumen de este estado B lo hallamos aplicando la ley de Boyle (caso particular de la ley de los gases ideales)
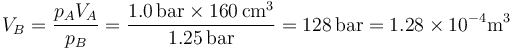
Esto quiere decir que la nueva altura del pistón es
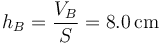
La presión ha aumentado en un 25% y el pistón ha bajado en un 20% de su anterior altura.
2.2 B→C
En el segundo proceso se aumenta la temperatura, pero el pistón puede moverse. Esto quiere decir que se trata de una expansión a presión constante. Gráficamente corresponde a un segmento horizontal en un diagrama pV.
El estado inicial B de este segmento ya lo tenemos
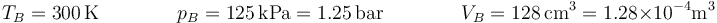
El final C lo hallamos teniendo en cuenta que su presión es la misma que la de B y su volumen el mismo que el iniciaL





