Trabajo en fusión de hielo
De Laplace
| (3 ediciones intermedias no se muestran.) | |||
| Línea 17: | Línea 17: | ||
por lo que, siendo la masa 1 kg el calor que entra en el sistema es simplemente | por lo que, siendo la masa 1 kg el calor que entra en el sistema es simplemente | ||
| - | <center><math>Q = (1\,\mathrm{kg}\times\left(333.55\frac{\mathrm{kJ}}{\mathrm{kg}}\right)=333.55\mathrm{kJ}</math></center> | + | <center><math>Q = (1\,\mathrm{kg}\times\left(333.55\frac{\mathrm{kJ}}{\mathrm{kg}}\right)=333.55\,\mathrm{kJ}</math></center> |
==Trabajo== | ==Trabajo== | ||
| + | De entrada puede parecer extraño que haya un trabajo en este proceso pues parece que al derretirse el hielo por calentamiento, nadie está haciendo fuerza sobre él, ni se está moviendo. | ||
| + | |||
| + | Pero no es así. Desde el mismo momento en que cambia el volumen, habiendo una presión externa, se está realizando trabajo. ¿Quién lo hace? El aire que rodea el hielo. Esa atmósfera de presión ejerce una fuerza sobre el hielo y lo comprime al pasar a la forma de agua. Si no estuviera el aire exterior, las moléculas de agua se desperdigarían y no formarían agua líquida. | ||
| + | |||
| + | El trabajo realizado a presión externa constante vale | ||
| + | |||
| + | <center><math>W = -p_\mathrm{ext}\,\Delta V = -p_\mathrm{ext}(V_2-V_1)</math></center> | ||
| + | |||
| + | Los volúmenes inicial y final los obtenemos de que conocemos la masa y la densidad. Para el hielo | ||
| + | |||
| + | <center><math>V_1 = \frac{m}{\rho_\mathrm{hielo}}=\frac{1\,\mathrm{kg}}{917\,\mathrm{kg}/\mathrm{m}^3}=1.091\times 10^{-3}\,\mathrm{m}^3</math></center> | ||
| + | |||
| + | y para el agua | ||
| + | |||
| + | <center><math>V_1 = \frac{m}{\rho_\mathrm{hielo}}=\frac{1\,\mathrm{kg}}{1000\,\mathrm{kg}/\mathrm{m}^3}=1.000\times 10^{-3}\,\mathrm{m}^3</math></center> | ||
| + | |||
| + | de forma que la variación del volumen es | ||
| + | |||
| + | <center><math>V_2 -V_1 = (1.000-1.091)\times 10^{3}\mathrm{m}^3 = -9.1\times 10^{-5}\,\mathrm{m}^3 = -91\,\mathrm{cm}^3</math></center> | ||
| + | |||
| + | Al fundirse el hielo, el volumen ocupado se reduce casi en un 10%. | ||
| + | |||
| + | El trabajo realizado vale | ||
| + | |||
| + | <center><math>W = -(1.013\times 10^5\mathrm{Pa})\times(-9.1\times 10^{-5}\mathrm{m}^3) = +9.2\,\mathrm{J}</math></center> | ||
| + | |||
| + | El trabajo es positivo ya que el aire exterior comprime al sistema. | ||
| + | |||
==Entalpía y energía interna== | ==Entalpía y energía interna== | ||
===Entalpía=== | ===Entalpía=== | ||
| + | En un proceso a presión constante, el calor que entra en el sistema es igual a la variación de la entalpía | ||
| + | |||
| + | <center><math>\Delta H = Q = 333.55\,\mathrm{kJ}</math></center> | ||
| + | |||
===Energía interna=== | ===Energía interna=== | ||
| + | La variación de la energía interna no coincide con el calor absorbido, al realizarse también trabajo sobre el sistema. Por el priner principio de la termodinámica | ||
| + | |||
| + | <center><math>\Delta U = Q + W = 333550\,\mathrm{J}+9.2\,\mathrm{J}\simeq 333.56\,\mathrm{kJ}</math></center> | ||
| + | |||
| + | Vemos que el trabajo realizado es ridículamente pequeño comparado con el calor, por lo que puede despreciarse. | ||
| + | |||
| + | No ocurre lo mismo en el caso del [[Calentamiento_de_agua_con_una_resistencia|paso de agua a vapor de agua]], donde el volumen ocupado se multiplica por 1700 (al pasar la densidad de 1000kg/m³ a 0.6 kg/m³) lo que supone un trabajo importante. | ||
| + | |||
[[Categoría:Problemas del primer principio de la termodinámica (GIE)]] | [[Categoría:Problemas del primer principio de la termodinámica (GIE)]] | ||
última version al 10:24 23 feb 2013
Contenido |
1 Enunciado
Tenemos 1 kg de hielo (densidad de masa 917 kg/m³) a 0 °C, al cual se le cede lentamente calor a una presión de 101.3 kPa hasta que convierte por completo en agua (densidad de masa 1000 kg/m³). Para este proceso, halle
- El calor que entra en el sistema
- El trabajo realizado sobre el sistema
- La variación de entalpía y de energía interna del sistema
2 Calor
A presión constante, el calor es proporcional a la masa que se derrite


por lo que, siendo la masa 1 kg el calor que entra en el sistema es simplemente
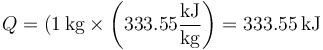
3 Trabajo
De entrada puede parecer extraño que haya un trabajo en este proceso pues parece que al derretirse el hielo por calentamiento, nadie está haciendo fuerza sobre él, ni se está moviendo.
Pero no es así. Desde el mismo momento en que cambia el volumen, habiendo una presión externa, se está realizando trabajo. ¿Quién lo hace? El aire que rodea el hielo. Esa atmósfera de presión ejerce una fuerza sobre el hielo y lo comprime al pasar a la forma de agua. Si no estuviera el aire exterior, las moléculas de agua se desperdigarían y no formarían agua líquida.
El trabajo realizado a presión externa constante vale
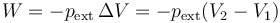
Los volúmenes inicial y final los obtenemos de que conocemos la masa y la densidad. Para el hielo
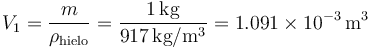
y para el agua

de forma que la variación del volumen es
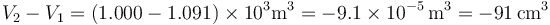
Al fundirse el hielo, el volumen ocupado se reduce casi en un 10%.
El trabajo realizado vale
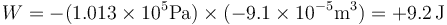
El trabajo es positivo ya que el aire exterior comprime al sistema.
4 Entalpía y energía interna
4.1 Entalpía
En un proceso a presión constante, el calor que entra en el sistema es igual a la variación de la entalpía
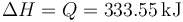
4.2 Energía interna
La variación de la energía interna no coincide con el calor absorbido, al realizarse también trabajo sobre el sistema. Por el priner principio de la termodinámica
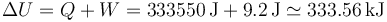
Vemos que el trabajo realizado es ridículamente pequeño comparado con el calor, por lo que puede despreciarse.
No ocurre lo mismo en el caso del paso de agua a vapor de agua, donde el volumen ocupado se multiplica por 1700 (al pasar la densidad de 1000kg/m³ a 0.6 kg/m³) lo que supone un trabajo importante.





