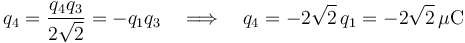Superposición de fuerzas electrostáticas (GIA)
De Laplace
(Diferencias entre revisiones)
(→Fuerza sobre la carga q_3) |
(→Enunciado) |
||
| (26 ediciones intermedias no se muestran.) | |||
| Línea 5: | Línea 5: | ||
# Calcular la fuerza sobre <math>q_3</math>. | # Calcular la fuerza sobre <math>q_3</math>. | ||
# ¿Qué valor ha de tener una carga <math>q_4</math> situada en el origen para que la fuerza neta sobre la partícula con carga <math>q_3</math> pase a ser nula? | # ¿Qué valor ha de tener una carga <math>q_4</math> situada en el origen para que la fuerza neta sobre la partícula con carga <math>q_3</math> pase a ser nula? | ||
| + | |||
| + | |||
| + | [[Categoría:Problemas de campo eléctrico F2 GIA]] | ||
==Solución== | ==Solución== | ||
===Fuerza sobre la carga <math>q_3</math>=== | ===Fuerza sobre la carga <math>q_3</math>=== | ||
| - | + | Las fuerzas que describen la interacción electrostática verifican el principio de superposición. En el sistema que nos ocupa, la <math>q_3</math> está sometida a la acción simultánea de las cargas <math>q_1</math> y <math>q_2</math>. La fuerza total <math>\vec{F}_3</math> que actúa sobre aquélla es igual a la suma vectorial de las fuerzas electrostáticas que cada una de las cargas <math>q_1</math> y <math>q_2</math> ejercerían por separado, y que verificarán la ley de Coulomb: | |
| + | |||
| + | [[Archivo:bol_1_3_1.gif|right]]<center><math>\vec{F}_3=\vec{F}_{31}+\vec{F}_{32}\,\mathrm{;}\quad\mbox{con}\quad\vec{F}_{3i}=\ k_e\!\ q_iq_3\ \frac{\vec{r}_3-\vec{r}_i}{|\vec{r}_3-\vec{r}_i|^3}\quad (i=1,2)</math></center> | ||
| + | |||
| + | Utilizando las expresiones analíticas de los vectores que indican las posiciones de las tres cargas, se obtiene: | ||
| + | |||
| + | <center><math>\vec{F}_3= k_e\!\ \frac{q_1q_3}{d^2}\ \vec{\jmath}+k_e\!\ \frac{q_2q_3}{d^2}\ \vec{\imath}=k_e\!\ \frac{q_3}{d^2}\ \bigg(q_2\!\ \vec{\imath}+q_1\!\ \vec{\jmath}\bigg)</math></center> | ||
| + | |||
| + | Y como las cargas <math>q_1</math> y <math>q_2</math> son idénticas, se tendrá que las componentes cartesianas de la fuerza total so iguales: | ||
| + | |||
| + | <center><math>F_3^x=F_3^y\approx 18\times 10^{-3}\,N</math></center> | ||
| + | |||
| + | ===Carga que anula la interacción sobre <math>q_3</math>=== | ||
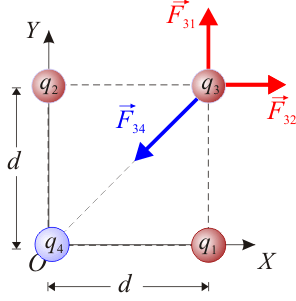
| + | Una carga <math>q_4</math> en el origen del sistema de referencia ejercería una fuerza | ||
| + | <center><math>\vec{F}_{34}= k_e\!\ q_4q_3\ \frac{\vec{r}_3}{|\vec{r}_3|^3}= k_e\!\ \frac{q_4q_3}{2\sqrt{2}\!\ d^2}\ \bigg(\vec{\imath}+\vec{\jmath}\bigg)</math></center> | ||
| + | |||
| + | [[Archivo:bol_1_3_2.gif|right]]sobre la carga <math>q_3</math>. Si esta interacción se superpone con la de las cargas <math>q_1</math> y <math>q_2</math>, la fuerza total que actúa sobre aquélla será ahora: | ||
| + | |||
| + | <center><math>\vec{F}_3^\prime=\vec{F}_{31}+\vec{F}_{32}+\vec{F}_{34}</math></center> | ||
| + | |||
| + | Y para que ésta sea nula se deberá cumplir: | ||
| + | |||
| + | <center><math>\vec{F}_3^\prime=\vec{0}\quad\Longleftrightarrow\quad\vec{F}_{34}=-(\vec{F}_{31}+\vec{F}_{32})=-\vec{F}_3=- k_e\!\ \frac{q_1q_3}{d^2}\ \bigg(\vec{\imath}+\vec{\jmath}\bigg)</math></center> | ||
| + | |||
| + | donde hemos tenido en cuenta que las cargas <math>q_1</math> y <math>q_2</math> son idénticas. Y para que ésta sea la fuerza ejercicia por la carga <math>q_4</math> se deberá cumplir... | ||
| - | + | <center><math>q_4=\frac{q_4q_3}{2\sqrt{2}}=-q_1q_3\quad\Longrightarrow\quad q_4=-2\sqrt{2}\!\ q_1=-2\sqrt{2}\,\mu\mathrm{C}</math></center> | |
última version al 00:19 11 feb 2013
Contenido |
1 Enunciado
Dos partículas con cargas eléctricas q1 = q2 = 1μC se encuentran situadas en las posiciones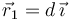 
y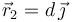 
, siendo 
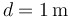. Se coloca una tercera partícula con carga 
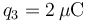en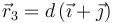 
.
- Calcular la fuerza sobre q3.
- ¿Qué valor ha de tener una carga q4 situada en el origen para que la fuerza neta sobre la partícula con carga q3 pase a ser nula?
2 Solución
2.1 Fuerza sobre la carga q3
Las fuerzas que describen la interacción electrostática verifican el principio de superposición. En el sistema que nos ocupa, la q3 está sometida a la acción simultánea de las cargas q1 y q2. La fuerza total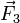 
que actúa sobre aquélla es igual a la suma vectorial de las fuerzas electrostáticas que cada una de las cargas q1 y q2 ejercerían por separado, y que verificarán la ley de Coulomb:
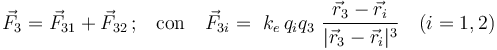
Utilizando las expresiones analíticas de los vectores que indican las posiciones de las tres cargas, se obtiene:
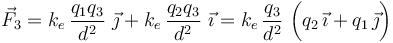
Y como las cargas q1 y q2 son idénticas, se tendrá que las componentes cartesianas de la fuerza total so iguales:
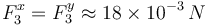
2.2 Carga que anula la interacción sobre q3
Una carga q4 en el origen del sistema de referencia ejercería una fuerza
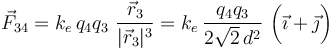
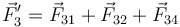
Y para que ésta sea nula se deberá cumplir:
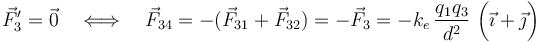
donde hemos tenido en cuenta que las cargas q1 y q2 son idénticas. Y para que ésta sea la fuerza ejercicia por la carga q4 se deberá cumplir...
