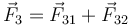Superposición de fuerzas electrostáticas (GIA)
De Laplace
(Diferencias entre revisiones)
(→Fuerza sobre la carga q_3) |
(→Fuerza sobre la carga q_3) |
||
| Línea 8: | Línea 8: | ||
==Solución== | ==Solución== | ||
===Fuerza sobre la carga <math>q_3</math>=== | ===Fuerza sobre la carga <math>q_3</math>=== | ||
| - | + | Las fuerzas que describen la interacción electrostática verifican el principio de superposición. En el sistema que nos ocupa, la <math>q_3</math> está sometida a la acción simultánea de las cargas <math>q_1</math> y <math>q_2</math>. La fuerza total <math>\vec{F}_3</math> que actúa sobre aquélla es igual a la suma vectorial de las fuerzas que cada una de las cargas <math>q_1</math> y <math>q_2</math> ejercerían por separado: | |
[[Archivo:bol_1_3_1.gif|right]]<center><math>\vec{F}_3=\vec{F}_{31}+\vec{F}_{32}</math></center> | [[Archivo:bol_1_3_1.gif|right]]<center><math>\vec{F}_3=\vec{F}_{31}+\vec{F}_{32}</math></center> | ||
Revisión de 23:01 10 feb 2013
1 Enunciado
Dos partículas con cargas eléctricas q1 = q2 = 1μC se encuentran situadas en las posiciones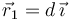 
y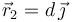 
, siendo 
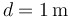. Se coloca una tercera partícula con carga 
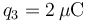en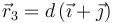 
.
- Calcular la fuerza sobre q3.
- ¿Qué valor ha de tener una carga q4 situada en el origen para que la fuerza neta sobre la partícula con carga q3 pase a ser nula?
2 Solución
2.1 Fuerza sobre la carga q3
Las fuerzas que describen la interacción electrostática verifican el principio de superposición. En el sistema que nos ocupa, la q3 está sometida a la acción simultánea de las cargas q1 y q2. La fuerza total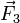 
que actúa sobre aquélla es igual a la suma vectorial de las fuerzas que cada una de las cargas q1 y q2 ejercerían por separado:
