Rapidez de los puntos de un tornillo
De Laplace
(→Enunciado) |
|||
| (Una edición intermedia no se muestra.) | |||
| Línea 2: | Línea 2: | ||
Un tornillo de radio 2 mm y paso de rosca 1 mm avanza impulsado por un destornillador de forma que su punta se mueve a 2 mm/s. Determine la rapidez de los puntos del filete del tornillo. | Un tornillo de radio 2 mm y paso de rosca 1 mm avanza impulsado por un destornillador de forma que su punta se mueve a 2 mm/s. Determine la rapidez de los puntos del filete del tornillo. | ||
| - | + | <center>[[Archivo:tornillo.png]]</center> | |
| + | |||
==Solución== | ==Solución== | ||
El tornillo realiza un movimiento helicoidal permanente. La rapidez de los puntos del filete es de la forma | El tornillo realiza un movimiento helicoidal permanente. La rapidez de los puntos del filete es de la forma | ||
última version al 22:11 12 ene 2013
1 Enunciado
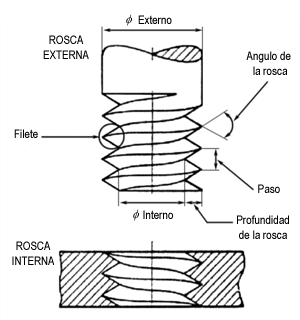
Un tornillo de radio 2 mm y paso de rosca 1 mm avanza impulsado por un destornillador de forma que su punta se mueve a 2 mm/s. Determine la rapidez de los puntos del filete del tornillo.
2 Solución
El tornillo realiza un movimiento helicoidal permanente. La rapidez de los puntos del filete es de la forma
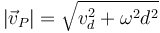
siendo vd la velocidad de avance del tornillo (2 mm/s), d es la distancia del filete al eje del tornillo (2 mm) y ω es la velocidad angular, que aun no conocemos.
El valor de ω lo sacamos de que los puntos del filete describen una hélice, de forma que en el tiempo que dan una vuelta avanzan el paso de rosca b (1 mm). Por tanto
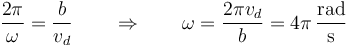
lo que nos da la rapidez
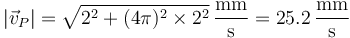
Vemos que la velocidad de estos puntos es mucho mayor que la de avance, y es que recorren una distancia mucho mayor que si se movieran en línea recta.





