Entrar Página Discusión Historial Go to the site toolbox

Fuerzas de frenado de un automóvil

De Laplace

(Diferencias entre revisiones)
(→Planteamiento del problema)
Línea 26: Línea 26:
<center><math>ma_C = F_{rA}+F_{rB}\qquad\qquad 0 = -mg + F_{nA}+F_{nB}</math></center>
<center><math>ma_C = F_{rA}+F_{rB}\qquad\qquad 0 = -mg + F_{nA}+F_{nB}</math></center>
 +
 +
la primera nos dice que, puesto que el coche está frenando (<math>a_C < 0</math>), las fuerzas de rozamiento sobre los ejes van hacia atrás. La segunda que, dado que el coche no se mueve verticalmente, las fuerzas normales compensan al peso.
 +
 +
Con estas ecuaciones no tenemos información suficiente para determinar las fuerzas, pues tenemos cuatro componentes y solo dos ecuaciones.
 +
 +
Una tercera ecuación la obtenemos del teorema del momento cinético. En este caso, el coche no esta volcando hacia adelante ni hacia atrás (lo que sería "hacer el caballito"). El coche simplemente se traslada. Esto quiere decir que el momento de las fuerzas respecto al centro de masas es nulo (ya que no hay aceleración angular)
 +
 +
<center><math>\vec{M}_C = \vec{0}</math></center>
 +
 +
En el sistema de fuerzas, el peso tiene momento nulo, por estar aplicado en el propio CM. Las fuerzas de rozamiento y la fuerza normal en el eje trasero producen un par en sentido horario, que tiende a volcar el coche hacia adelante. La única fuerza con un momento en sentido antihorario es la fuerza normal sobre el eje delantero, <math>F_{nA}</math>. Si este par es capaz de compensar al de las otras tres esto implica que la fuerza normal delantera es más intensa que la trasera, es decir, que como consecuencia de la aceleración horizontal se produce una diferencia en la fuerza vertical sobre los dos ejes (lo que tiene importancia de cara al diseño del freno y la suspensión del vehículo).
 +
 +
La ecuación del momento cinético queda
 +
 +
<center><math>\vec{0} = \overrightarrow{CA}\times\vec{F}_A + \overrightarrow{CB}\times\vec{F}_B</math></center>
 +
 +
Separamos en la fuerza normal y la de rozamiento
 +
 +
<center><math>\vec{0} = \overrightarrow{CA}\times\vec{F}_{nA} + \overrightarrow{CA}\times\vec{F}_{rA} + \overrightarrow{CB}\times\vec{F}_{nB}+\overrightarrow{CB}\times\vec{F}_{rB}</math></center>
 +
 +
Todas estos momentos tienen solo componente en la dirección de <math>\vec{k}</math> y el valor de cada uno es igual al producto de la fuerza por el brazo del par (distancia del CM a la recta de aplicación de cada una), con un signo que indica si el momento es en sentido horario o antihorario.
 +
 +
<center><math>\frac{D}{2}F_{nA}+HF_{rA}-\frac{D}{2}F_{nB}+HF_{rB}</math></center>
 +
 +
con H la altura del CM y D la distancia entre ejes (suponiendo, como indica el enunciado, que el CM está a medio camino entre los dos ejes). Podemos escribir esta ecuación en la forma
 +
 +
<center><math>F_{nA}-F_{nB}= -\frac{2H}{D}\left(F_{rA}+F_{rB}\right)</math></center>
 +
 +
Sabemos cuanto vale la suma de las fuerzas de rozamiento, por lo que
 +
 +
<center><math>F_{nA}-F_{nB}=-\frac{2H}{D}ma_c</math></center>
 +
 +
Esta ecuación, junto con
 +
 +
<center><math>F_{nA}+F_{nB}=mg\,</math></center>
 +
 +
nos da las dos fuerzas normales
 +
 +
<center><math>F_{nA}=\frac{mg}{2}\left(1-\frac{2Ha_C}{Dg}\right)\qquad\qquad F_{nB}=\frac{mg}{2}\left(1+\frac{2Ha_C}{Dg}\right)</math></center>
 +
 +
Teniendo en cuenta que <math>a_C</math> es negativa, llegamos a que la fuerza sobre el eje delantero supera a la del trasero. A la inversa ocurre cuando el coche acelera, en ese caso es el eje trasero el que recibe la sobrecarga.
 +
 +
Sustituyendo los valores numéricos obtenemos estas dos fuerzas normales
 +
 +
\frac{2Ha_c}{Dg}= \frac
 +
 +
 +
 +
[[Categoría:Problemas de dinámica del sólido rígido (GIE)]]
[[Categoría:Problemas de dinámica del sólido rígido (GIE)]]

Revisión de 23:15 8 ene 2013

1 Enunciado

Un coche tiene una masa 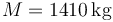M= 1410\,\mathrm{kg} y distancia entre ejes 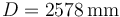D=2578\,\mathrm{mm} frena con una aceleración de 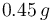0.45\,g. Si su centro de masas se encuentra a mitad de camino entre los dos ejes y a 90 cm de altura y las fuerzas de rozamiento en cada rueda son proporcionales a las fuerzas normales que se ejerce sobre cada una, ¿en cuál de los dos ejes se ejerce una mayor fuerza al frenar? ¿Cuánto vale aproximadamente la fuerza sobre cada eje?

2 Introducción

En lo que sigue consideraremos que el coche se mueve en línea recta y que el problema es bidimensional en el plano XY, con X el eje horizontal, tangente al suelo e Y el vertical, dirección en la que actúa el peso.

Por simplicidad, consideraremos la fuerza sobre el eje delantero como un todo, pero en realidad las fuerzas de contacto se ejercen sobre las ruedas, por lo que cuando se dice que sobre el eje delantero se aplica una fuerza F, lo que se quiere decir es que sobre cada rueda delantera se aplica una fuerza F/2. Si el coche estuviera describiendo una curva, las fuerzas sobre las ruedas interiores y exteriores serían asimétricas. Nos limitaremos aquí al caso más simple del movimiento rectilíneo.

3 Planteamiento del problema

Sobre el coche actúan tres fuerzas (cinco, en realidad, según hemos dicho antes):

  • El peso, que se aplica sobre el centro de masas
  • La fuerza sobre el eje delantero
  • La fuerza sobre el eje trasero

A su vez, estas dos fuerzas se descomponen en dos

  • Una fuerza normal al plano horizontal
  • Una fuerza de rozamiento tangente a este plano.

Si denominamos A al punto de contacto del eje delantero con el suelo, B al trasero y C al centro de masas, el teorema de la cantidad de movimiento queda

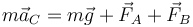
m\vec{a}_C = m\vec{g}+\vec{F}_A+\vec{F}_B

Separando en las dos componentes cartesianas nos queda

ma_C = F_{rA}+F_{rB}\qquad\qquad 0 = -mg + F_{nA}+F_{nB}

la primera nos dice que, puesto que el coche está frenando (aC < 0), las fuerzas de rozamiento sobre los ejes van hacia atrás. La segunda que, dado que el coche no se mueve verticalmente, las fuerzas normales compensan al peso.

Con estas ecuaciones no tenemos información suficiente para determinar las fuerzas, pues tenemos cuatro componentes y solo dos ecuaciones.

Una tercera ecuación la obtenemos del teorema del momento cinético. En este caso, el coche no esta volcando hacia adelante ni hacia atrás (lo que sería "hacer el caballito"). El coche simplemente se traslada. Esto quiere decir que el momento de las fuerzas respecto al centro de masas es nulo (ya que no hay aceleración angular)

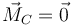
\vec{M}_C = \vec{0}

En el sistema de fuerzas, el peso tiene momento nulo, por estar aplicado en el propio CM. Las fuerzas de rozamiento y la fuerza normal en el eje trasero producen un par en sentido horario, que tiende a volcar el coche hacia adelante. La única fuerza con un momento en sentido antihorario es la fuerza normal sobre el eje delantero, FnA. Si este par es capaz de compensar al de las otras tres esto implica que la fuerza normal delantera es más intensa que la trasera, es decir, que como consecuencia de la aceleración horizontal se produce una diferencia en la fuerza vertical sobre los dos ejes (lo que tiene importancia de cara al diseño del freno y la suspensión del vehículo).

La ecuación del momento cinético queda

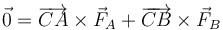
\vec{0} = \overrightarrow{CA}\times\vec{F}_A + \overrightarrow{CB}\times\vec{F}_B

Separamos en la fuerza normal y la de rozamiento

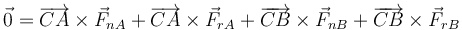
\vec{0} = \overrightarrow{CA}\times\vec{F}_{nA} + \overrightarrow{CA}\times\vec{F}_{rA} + \overrightarrow{CB}\times\vec{F}_{nB}+\overrightarrow{CB}\times\vec{F}_{rB}

Todas estos momentos tienen solo componente en la dirección de \vec{k} y el valor de cada uno es igual al producto de la fuerza por el brazo del par (distancia del CM a la recta de aplicación de cada una), con un signo que indica si el momento es en sentido horario o antihorario.

\frac{D}{2}F_{nA}+HF_{rA}-\frac{D}{2}F_{nB}+HF_{rB}

con H la altura del CM y D la distancia entre ejes (suponiendo, como indica el enunciado, que el CM está a medio camino entre los dos ejes). Podemos escribir esta ecuación en la forma

F_{nA}-F_{nB}= -\frac{2H}{D}\left(F_{rA}+F_{rB}\right)

Sabemos cuanto vale la suma de las fuerzas de rozamiento, por lo que

F_{nA}-F_{nB}=-\frac{2H}{D}ma_c

Esta ecuación, junto con

F_{nA}+F_{nB}=mg\,

nos da las dos fuerzas normales

F_{nA}=\frac{mg}{2}\left(1-\frac{2Ha_C}{Dg}\right)\qquad\qquad F_{nB}=\frac{mg}{2}\left(1+\frac{2Ha_C}{Dg}\right)

Teniendo en cuenta que aC es negativa, llegamos a que la fuerza sobre el eje delantero supera a la del trasero. A la inversa ocurre cuando el coche acelera, en ese caso es el eje trasero el que recibe la sobrecarga.

Sustituyendo los valores numéricos obtenemos estas dos fuerzas normales

\frac{2Ha_c}{Dg}= \frac

Obtenido de "http://tesla.us.es/wiki/index.php/Fuerzas_de_frenado_de_un_autom%C3%B3vil"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace