Fuerzas de frenado de un automóvil
De Laplace
(Página creada con '==Enunciado== Un coche tiene una masa <math>M= 1410\,\mathrm{kg}</math> y distancia entre ejes <math>D=2578\,\mathrm{mm}</math> frena con una aceleración de <math>0.45\,g</math…') |
|||
| Línea 2: | Línea 2: | ||
Un coche tiene una masa <math>M= 1410\,\mathrm{kg}</math> y distancia entre ejes <math>D=2578\,\mathrm{mm}</math> frena con una aceleración de <math>0.45\,g</math>. Si su centro de masas se encuentra a mitad de camino entre los dos ejes y a 90 cm de altura y las fuerzas de rozamiento en cada rueda son proporcionales a las fuerzas | Un coche tiene una masa <math>M= 1410\,\mathrm{kg}</math> y distancia entre ejes <math>D=2578\,\mathrm{mm}</math> frena con una aceleración de <math>0.45\,g</math>. Si su centro de masas se encuentra a mitad de camino entre los dos ejes y a 90 cm de altura y las fuerzas de rozamiento en cada rueda son proporcionales a las fuerzas | ||
normales que se ejerce sobre cada una, ¿en cuál de los dos ejes se ejerce una mayor fuerza al frenar? ¿Cuánto vale aproximadamente la fuerza sobre cada eje? | normales que se ejerce sobre cada una, ¿en cuál de los dos ejes se ejerce una mayor fuerza al frenar? ¿Cuánto vale aproximadamente la fuerza sobre cada eje? | ||
| - | == | + | ==Introducción== |
| + | En lo que sigue consideraremos que el coche se mueve en línea recta y que el problema es bidimensional en el plano XY, con X el eje horizontal, tangente al suelo e Y el vertical, dirección en la que actúa el peso. | ||
| + | |||
| + | Por simplicidad, consideraremos la fuerza sobre el eje delantero como un todo, pero en realidad las fuerzas de contacto se ejercen sobre las ruedas, por lo que cuando se dice que sobre el eje delantero se aplica una fuerza F, lo que se quiere decir es que sobre cada rueda delantera se aplica una fuerza F/2. Si el coche estuviera describiendo una curva, las fuerzas sobre las ruedas interiores y exteriores serían asimétricas. Nos limitaremos aquí al caso más simple del movimiento rectilíneo. | ||
| + | |||
| + | ==Planteamiento del problema== | ||
| + | Sobre el coche actúan tres fuerzas (cinco, en realidad, según hemos dicho antes): | ||
| + | |||
| + | * El peso, que se aplica sobre el centro de masas | ||
| + | * La fuerza sobre el eje delantero | ||
| + | * La fuerza sobre el eje trasero | ||
| + | |||
| + | A su vez, estas dos fuerzas se descomponen en dos | ||
| + | |||
| + | * Una fuerza normal al plano horizontal | ||
| + | * Una fuerza de rozamiento tangente a este plano. | ||
| + | |||
| + | Si denominamos A al punto de contacto del eje delantero con el suelo, B al trasero y C al centro de masas, el teorema de la cantidad de movimiento queda | ||
| + | |||
| + | <center><math>m\vec{a}_C = m\vec{g}+\vec{F}_A+\vec{F}_B</math></center> | ||
| + | |||
| + | Separando en las dos componentes cartesianas nos queda | ||
| + | |||
| + | <center><math>ma_C = F_{rA}+F_{rB}\qquad\qquad 0 = -mg + F_{nA}+F_{nB}</math></center> | ||
[[Categoría:Problemas de dinámica del sólido rígido (GIE)]] | [[Categoría:Problemas de dinámica del sólido rígido (GIE)]] | ||
Revisión de 22:24 8 ene 2013
1 Enunciado
Un coche tiene una masa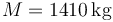 
y distancia entre ejes 
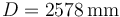frena con una aceleración de 
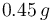. Si su centro de masas se encuentra a mitad de camino entre los dos ejes y a 90 cm de altura y las fuerzas de rozamiento en cada rueda son proporcionales a las fuerzas
normales que se ejerce sobre cada una, ¿en cuál de los dos ejes se ejerce una mayor fuerza al frenar? ¿Cuánto vale aproximadamente la fuerza sobre cada eje?
2 Introducción
En lo que sigue consideraremos que el coche se mueve en línea recta y que el problema es bidimensional en el plano XY, con X el eje horizontal, tangente al suelo e Y el vertical, dirección en la que actúa el peso.
Por simplicidad, consideraremos la fuerza sobre el eje delantero como un todo, pero en realidad las fuerzas de contacto se ejercen sobre las ruedas, por lo que cuando se dice que sobre el eje delantero se aplica una fuerza F, lo que se quiere decir es que sobre cada rueda delantera se aplica una fuerza F/2. Si el coche estuviera describiendo una curva, las fuerzas sobre las ruedas interiores y exteriores serían asimétricas. Nos limitaremos aquí al caso más simple del movimiento rectilíneo.
3 Planteamiento del problema
Sobre el coche actúan tres fuerzas (cinco, en realidad, según hemos dicho antes):
- El peso, que se aplica sobre el centro de masas
- La fuerza sobre el eje delantero
- La fuerza sobre el eje trasero
A su vez, estas dos fuerzas se descomponen en dos
- Una fuerza normal al plano horizontal
- Una fuerza de rozamiento tangente a este plano.
Si denominamos A al punto de contacto del eje delantero con el suelo, B al trasero y C al centro de masas, el teorema de la cantidad de movimiento queda
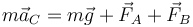
Separando en las dos componentes cartesianas nos queda
