Rodadura y deslizamiento de un disco
De Laplace
(→Casos particulares) |
(→Introducción) |
||
| Línea 13: | Línea 13: | ||
==Introducción== | ==Introducción== | ||
| + | Este es un movimiento sobre el plano XZ y por tanto, el estudio de la cinemática se reduce a dos dimensiones. Para todos los puntos del disco se cumplirá que | ||
| + | |||
| + | <center><math>\vec{v}=v_x\vec{\imath}+v_z\vec{k}</math></center> | ||
| + | |||
| + | con <math>v_x</math> y <math>v_z</math> las componentes cartesianas de la velocidad (que serán dependientes de la posición). Asimismo, la velocidad angular será perpendicular al plano del movimiento y por tanto irá en la dirección del eje OY | ||
| + | |||
| + | <center><math>\vec{\omega}=\omega\vec{\jmath}</math></center> | ||
| + | |||
| + | Esta velocidad angular es independiente de la posición (aunque variará en cada caso particular). | ||
| + | |||
| + | Al ser la velocidad angular ortogonal a las velocidades lineales, los movimientos posibles serán de reposo, traslación y rotación, pero nunca helicoidales. | ||
| + | |||
==Velocidad angular== | ==Velocidad angular== | ||
==Velocidades lineales== | ==Velocidades lineales== | ||
Revisión de 11:32 20 dic 2012
Contenido |
1 Enunciado
Un disco de radio R y masa M rueda y desliza sobre el plano horizontal z = 0 de forma que la velocidad del punto de contacto con el suelo, A, y del diametralmente opuesto, B son de la forma

- Calcule la velocidad angular del disco.
- Halle la velocidad del centro del disco, C, así como de los puntos D y E situados en los extremos de un diámetro horizontal.
- Determine la posición del centro instantáneo de rotación.
- Indique a qué se reducen los resultados anteriores en los casos particulares siguientes:
- vA = − vB
- vA = 0
- vA = vB
2 Introducción
Este es un movimiento sobre el plano XZ y por tanto, el estudio de la cinemática se reduce a dos dimensiones. Para todos los puntos del disco se cumplirá que
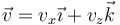
con vx y vz las componentes cartesianas de la velocidad (que serán dependientes de la posición). Asimismo, la velocidad angular será perpendicular al plano del movimiento y por tanto irá en la dirección del eje OY

Esta velocidad angular es independiente de la posición (aunque variará en cada caso particular).
Al ser la velocidad angular ortogonal a las velocidades lineales, los movimientos posibles serán de reposo, traslación y rotación, pero nunca helicoidales.





