Centro de masas en sistemas de esferas
De Laplace
(→Una esfera con hueco) |
|||
| Línea 8: | Línea 8: | ||
==Dos esferas adyacentes== | ==Dos esferas adyacentes== | ||
| + | El centro de masas de un sistema de partículas se calcula mediante la expreisón | ||
| + | |||
| + | <center><math>\vec{r}_C=\frac{\sum_i m_i\vec{r}_i}{M}=\frac{m_1\vec{r}_1+m_2\vec{r}_2+\cdots}{m_1+m_2+...}</math></center> | ||
| + | |||
| + | En el caso de que tengamos una distribución continua, esta fórmula se sustituye por la correspondiente integral | ||
| + | |||
| + | <center><math>\vec{r}_C=\frac{1}{M}\int_M \vec{r}_\mathrm{d}m = \frac{1}{M}\int_V \rho\,\vec{r}\,\mathrm{d}V</math></center> | ||
| + | |||
| + | En principio, para calcular el centro de masas del conjunto de las dos esferas debemos hacer la integral sobre el volumen completo. Sin embargo, el problema se simplifica si lo descomponemos en las dos partes que lo componen. | ||
| + | |||
| + | ===Masas=== | ||
| + | En primer lugar tenemos que la masa total del conjunto es la suma de las masas de cada una de las esferas | ||
| + | |||
| + | <center><math>M = M_1+M_2 = \int_{V_1}\rho_1\,\mathrm{d}V+\int_{V_2}\rho_2\,\mathrm{d}V</math></center> | ||
| + | |||
| + | En este caso las dos densidades son homogéneas (independientes de la posición) e iguales en las dos esferas, por lo que | ||
| + | |||
| + | <center><math>M_1 = \int_{V_1}\rho_1\,\mathrm{d}V = \rho_0V_1 = \frac{4\pi}{3}\rho_0R^3</math>{{qquad}}<math>M_2 = \int_{V_2}\rho_2\,\mathrm{d}V = \rho_0V_2 = \frac{4\pi}{3}\rho_0\left(\frac{R}{2}\right)^3=\frac{M_1}{8}</math></center> | ||
| + | |||
| + | siendo la masa total | ||
| + | |||
| + | <center><math>M=M_1+M_2=M_1+\frac{M_1}{8}=\frac{9}{8}M_1</math></center> | ||
| + | |||
| + | ===Centro de masas=== | ||
| + | Para el numerador que aparece en el centro de masas realizamos una descomposición similar y nos queda | ||
| + | |||
| + | <center><math>M\vec{r}_c = \int_{V}\rho\,\vec{r}\,\mathrm{d}V = \int_{V_1}\rho_1\,\vec{r}\,\mathrm{d}V+\int_{V_2}\rho_2\,\vec{r}\,\mathrm{d}V</math></center> | ||
| + | |||
| + | Ahora bien, los centros de masas de cada una de las esferas por separado verifican | ||
| + | |||
| + | <center><math>\vec{r}_{C1}=\frac{1}{M_1}\int_{V_1}\rho_1\vec{r}\mathrm{d}V\qquad\qquad \vec{r}_{C2}=\frac{1}{M_2}\int_{V_2}\rho_1\vec{r}\mathrm{d}V</math></center> | ||
| + | |||
| + | y por tanto | ||
| + | |||
| + | <center><math>M\vec{r}_C=M_1\vec{r}_{C1}+M_2\vec{r}_{C2}\qquad\Rightarrow\qquad \vec{r}_{C}=\frac{M_1\vec{r}_{C1}+M_2\vec{r}_{C2}}{M_1+M_2}</math></center> | ||
| + | |||
==Una esfera con hueco== | ==Una esfera con hueco== | ||
[[Categoría:Problemas de dinámica de los sistemas de partículas (GIE)]] | [[Categoría:Problemas de dinámica de los sistemas de partículas (GIE)]] | ||
Revisión de 19:17 15 dic 2012
Contenido |
1 Enunciado
Se tienen dos esferas macizas del mismo material de densidad homogénea, ρ0, una de ellas de radio R y la otra de radio R / 2. Las dos esferas son adyacentes. Determine la posición del centro de masas del sistema.
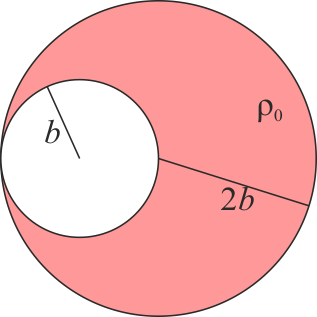
Si en lugar del sistema anterior se tiene una sola esfera maciza de radio R y densidad homogénea ρ0 en la que se ha horadado una cavidad también esférica, de radio R / 2, cuyo centro se encuentra a una distancia R / 2 del centro de la esfera original ¿dónde se halla el centro de masas del sólido?
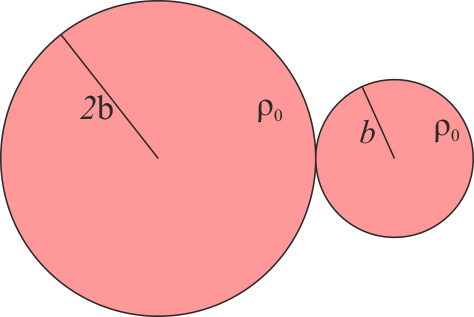
2 Dos esferas adyacentes
El centro de masas de un sistema de partículas se calcula mediante la expreisón
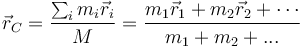
En el caso de que tengamos una distribución continua, esta fórmula se sustituye por la correspondiente integral
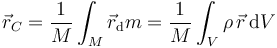
En principio, para calcular el centro de masas del conjunto de las dos esferas debemos hacer la integral sobre el volumen completo. Sin embargo, el problema se simplifica si lo descomponemos en las dos partes que lo componen.
2.1 Masas
En primer lugar tenemos que la masa total del conjunto es la suma de las masas de cada una de las esferas
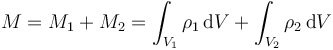
En este caso las dos densidades son homogéneas (independientes de la posición) e iguales en las dos esferas, por lo que


siendo la masa total
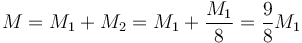
2.2 Centro de masas
Para el numerador que aparece en el centro de masas realizamos una descomposición similar y nos queda

Ahora bien, los centros de masas de cada una de las esferas por separado verifican

y por tanto






