Entrar Página Discusión Historial Go to the site toolbox

Conservación de magnitudes en movimiento curvo

De Laplace

(Diferencias entre revisiones)
(→Fuerza)
(→Fuerza)
Línea 29: Línea 29:
<center><math>x = \rho\cos(\varphi) = A\,\mathrm{sen}(\Omega t)\cos(\Omega t)\qquad \qquad y = \rho\,\mathrm{sen}(\varphi)=A\,\mathrm{sen}^2(\Omega t)</math></center>
<center><math>x = \rho\cos(\varphi) = A\,\mathrm{sen}(\Omega t)\cos(\Omega t)\qquad \qquad y = \rho\,\mathrm{sen}(\varphi)=A\,\mathrm{sen}^2(\Omega t)</math></center>
 +
 +
Derivando una vez tenemos las componentes cartesianas de la velocidad
 +
 +
<center><math>v_x = \dot{x} = A\Omega\left(\cos^2(\Omega t)-\mathrm{sen}^2(\Omega t)\right) =A\Omega\cos(2\Omega t)\qquad v_y = \dot{y}=2A\Omega\,\mathrm{sen}(\Omega t)\cos(\Omega t)=A\Omega \,\mathrm{sen}(2\Omega t)</math></center>
 +
 +
y derivando una segunda vez las de la aceleración
 +
 +
<center><math>a_x=\ddot{x}=-2A\Omega^2\,\mathrm{sen}(\Omega t)\qquad\qquad a_y = \ddot{y}=2A\Omega^2 \cos(2\Omega t)</math></center>
 +
 +
lo que nos da la fuerza
 +
 +
<center><math>\vec{F}=m\vec{a}=mA\Omega^2(-\mathrm{sen}\left(2\Omega t)\vec{\imath}+\cos(2\omega t)\vec{\jmath}\right)</math></center>
==Impulso==
==Impulso==

Revisión de 20:44 24 nov 2012

Contenido

1 Enunciado

Una partícula de masa m describe el movimiento plano

\rho = A\,\mathrm{sen}(\Omega t)\qquad\varphi = \Omega t\qquad\qquad\ t \in(0,\pi/\Omega)
  1. Calcule la fuerza que actúa sobre la partícula en cualquier instante del intervalo.
  2. Halle el impulso que experimenta entre t = 0 y t = π / (2Ω).
  3. Demuestre que el momento cinético de la partícula respecto al origen no se conserva, pero respecto al punto 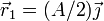\vec{r}_1 = (A/2)\vec{\jmath} sí.
  4. Calcule la energía cinética de la partícula. ¿Se conserva esta cantidad?

2 Fuerza

Podemos calcular la fuerza aplicando la segunda ley de Newton

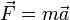
\vec{F}=m\vec{a}

que en coordenadas polares se escribe

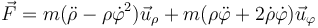
\vec{F}=m(\ddot{\rho}-\rho\dot{\varphi}^2)\vec{u}_\rho+m(\rho\ddot{\varphi}+2\dot{\rho}\dot{\varphi})\vec{u}_{\varphi}

Las derivadas de las dos coordenadas valen

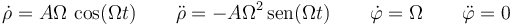
\dot{\rho}=A\Omega\,\cos(\Omega t)\qquad\ddot{\rho}=-A\Omega^2\,\mathrm{sen}(\Omega t)\qquad\dot{\varphi}=\Omega \qquad\ddot{\varphi}=0

lo que nos da la fuerza

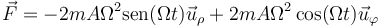
\vec{F}=-2mA\Omega^2\mathrm{sen}(\Omega t)\vec{u}_\rho + 2mA\Omega^2\cos(\Omega t)\vec{u}_\varphi

Alternativamente podemos expresar en primer lugar la posición en coordenadas cartesianas

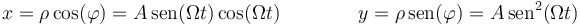
x = \rho\cos(\varphi) = A\,\mathrm{sen}(\Omega t)\cos(\Omega t)\qquad \qquad y = \rho\,\mathrm{sen}(\varphi)=A\,\mathrm{sen}^2(\Omega t)

Derivando una vez tenemos las componentes cartesianas de la velocidad

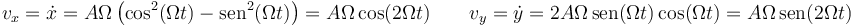
v_x = \dot{x} = A\Omega\left(\cos^2(\Omega t)-\mathrm{sen}^2(\Omega t)\right) =A\Omega\cos(2\Omega t)\qquad v_y = \dot{y}=2A\Omega\,\mathrm{sen}(\Omega t)\cos(\Omega t)=A\Omega \,\mathrm{sen}(2\Omega t)

y derivando una segunda vez las de la aceleración

a_x=\ddot{x}=-2A\Omega^2\,\mathrm{sen}(\Omega t)\qquad\qquad a_y = \ddot{y}=2A\Omega^2 \cos(2\Omega t)

lo que nos da la fuerza

\vec{F}=m\vec{a}=mA\Omega^2(-\mathrm{sen}\left(2\Omega t)\vec{\imath}+\cos(2\omega t)\vec{\jmath}\right)

3 Impulso

4 Momento cinético

5 Energía cinética

Obtenido de "http://tesla.us.es/wiki/index.php/Conservaci%C3%B3n_de_magnitudes_en_movimiento_curvo"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace