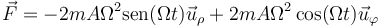Conservación de magnitudes en movimiento curvo
De Laplace
(Diferencias entre revisiones)
| Línea 17: | Línea 17: | ||
<center><math>\vec{F}=m(\ddot{\rho}-\rho\dot{\varphi}^2)\vec{u}_\rho+m(\rho\ddot{\varphi}+2\dot{\rho}\dot{\varphi})\vec{u}_{\varphi}</math></center> | <center><math>\vec{F}=m(\ddot{\rho}-\rho\dot{\varphi}^2)\vec{u}_\rho+m(\rho\ddot{\varphi}+2\dot{\rho}\dot{\varphi})\vec{u}_{\varphi}</math></center> | ||
| + | |||
| + | Las derivadas de las dos coordenadas valen | ||
| + | |||
| + | <center><math>\dot{\rho}=A\Omega\,\cos(\Omega t)\qquad\ddot{\rho}=-A\Omega^2\,\mathrm{sen}(\Omega t)\qquad\dot{\varphi}=\Omega \qquad\ddot{\varphi}=0</math></center> | ||
| + | |||
| + | lo que nos da la fuerza | ||
| + | |||
| + | <center><math>\vec{F}=-2mA\Omega^2\mathrm{sen}(\Omega t)\vec{u}_\rho + 2mA\Omega^2\cos(\Omega t)\vec{u}_\varphi</math></center> | ||
==Impulso== | ==Impulso== | ||
==Momento cinético== | ==Momento cinético== | ||
==Energía cinética== | ==Energía cinética== | ||
[[Categoría:Problemas de energía y leyes de conservación (GIE)]] | [[Categoría:Problemas de energía y leyes de conservación (GIE)]] | ||
Revisión de 19:14 24 nov 2012
Contenido |
1 Enunciado
Una partícula de masa m describe el movimiento plano

- Calcule la fuerza que actúa sobre la partícula en cualquier instante del intervalo.
- Halle el impulso que experimenta entre t = 0 y t = π / (2Ω).
- Demuestre que el momento cinético de la partícula respecto al origen no se conserva, pero respecto al punto
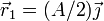 sí.
sí.
- Calcule la energía cinética de la partícula. ¿Se conserva esta cantidad?
2 Fuerza
Podemos calcular la fuerza aplicando la segunda ley de Newton
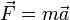
que en coordenadas polares se escribe
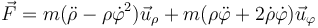
Las derivadas de las dos coordenadas valen
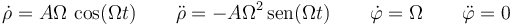
lo que nos da la fuerza