6.4. Disco rodando en pared (Ex.Sep/12)
De Laplace
(→Determinación gráfica de los centros instantáneos de rotación) |
(→Enunciado) |
||
| Línea 7: | Línea 7: | ||
Como parámetro descriptivo de la posición del sistema, se define el ángulo <math>\theta\,</math> que forma la barra <math>BC\,</math> con respecto a la vertical (ver figura). Se pide: | Como parámetro descriptivo de la posición del sistema, se define el ángulo <math>\theta\,</math> que forma la barra <math>BC\,</math> con respecto a la vertical (ver figura). Se pide: | ||
| - | # Determinar gráficamente la posición de los tres centros instantáneos de rotación: <math>I_{21}\,</math>, <math>I_{20}\,</math> | + | # Determinar gráficamente la posición de los tres centros instantáneos de rotación: <math>I_{21}\,</math>, <math>I_{20}\,</math> y <math>I_{01}\,</math>. |
# Calcular todas las velocidades angulares en función de la posición, es decir: <math>\vec{\omega}_{21}(\theta)\,,</math> <math>\vec{\omega}_{01}(\theta)\,</math> y <math>\vec{\omega}_{20}(\theta)\,</math>. | # Calcular todas las velocidades angulares en función de la posición, es decir: <math>\vec{\omega}_{21}(\theta)\,,</math> <math>\vec{\omega}_{01}(\theta)\,</math> y <math>\vec{\omega}_{20}(\theta)\,</math>. | ||
# Calcular las aceleraciones <math>\vec{a}^{\, C}_{01}\,</math> y <math>\vec{a}^{A}_{21}\,</math> (ver <math>A\,</math> en la figura). | # Calcular las aceleraciones <math>\vec{a}^{\, C}_{01}\,</math> y <math>\vec{a}^{A}_{21}\,</math> (ver <math>A\,</math> en la figura). | ||
Revisión de 15:26 13 nov 2012
Contenido |
1 Enunciado
El plano vertical fijo 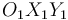 (sólido "1") de la figura contiene en todo instante a dos sólidos vinculados entre sí y en movimiento: un disco de radio
(sólido "1") de la figura contiene en todo instante a dos sólidos vinculados entre sí y en movimiento: un disco de radio  (sólido "2"), y una barra
(sólido "2"), y una barra 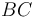 de longitud
de longitud  (sólido "0"). El disco rueda sin deslizar sobre el eje vertical
(sólido "0"). El disco rueda sin deslizar sobre el eje vertical 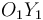 , avanzando su centro
, avanzando su centro  con velocidad constante
con velocidad constante 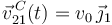 . Y, como consecuencia, también la barra se mueve, ya que su extremo
. Y, como consecuencia, también la barra se mueve, ya que su extremo  está articulado al
centro del disco, mientras que su extremo
está articulado al
centro del disco, mientras que su extremo  está articulado a un deslizador que lo obliga a recorrer el eje
está articulado a un deslizador que lo obliga a recorrer el eje 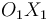 .
.
Como parámetro descriptivo de la posición del sistema, se define el ángulo  que forma la barra
que forma la barra 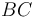 con respecto a la vertical (ver figura). Se pide:
con respecto a la vertical (ver figura). Se pide:
- Determinar gráficamente la posición de los tres centros instantáneos de rotación:
 ,
, 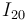 y
y 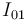 .
.
- Calcular todas las velocidades angulares en función de la posición, es decir:
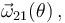
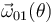 y
y 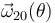 .
.
- Calcular las aceleraciones
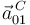 y
y 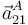 (ver
(ver  en la figura).
en la figura).
2 Determinación gráfica de los centros instantáneos de rotación
Se nos indica que el disco (sólido "2") rueda sin deslizar sobre el eje 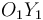 (sólido "1"). La ausencia de deslizamiento implica que el centro instantáneo de rotación del movimiento {21} coincide con el punto de contacto disco-eje:
(sólido "1"). La ausencia de deslizamiento implica que el centro instantáneo de rotación del movimiento {21} coincide con el punto de contacto disco-eje:
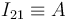
El extremo  de la barra (sólido "0") se halla articulado al centro del disco (sólido "2"). Por tanto, dicho punto
de la barra (sólido "0") se halla articulado al centro del disco (sólido "2"). Por tanto, dicho punto  es un punto fijo (centro permanente de rotación) en el movimiento {20}:
es un punto fijo (centro permanente de rotación) en el movimiento {20}:
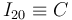
Dado que el extremo  de la barra (sólido "0") está obligado a recorrer el eje
de la barra (sólido "0") está obligado a recorrer el eje 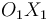 (sólido "1"), la velocidad
(sólido "1"), la velocidad 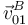 tiene necesariamente la dirección del eje
tiene necesariamente la dirección del eje 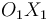 . Trazando la perpendicular a dicha velocidad en el punto
. Trazando la perpendicular a dicha velocidad en el punto  y trazando la recta que pasa por los puntos
y trazando la recta que pasa por los puntos  y
y 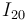 (en aplicación del teorema de los tres centros), hallaremos el punto
(en aplicación del teorema de los tres centros), hallaremos el punto 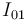 en la intersección de ambas rectas:
en la intersección de ambas rectas:
(ver I01 en la figura adjunta)







