3.9. Sonda espacial
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado==') |
(→Enunciado) |
||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| + | [[Archivo:sonda.png|right]] | ||
| + | |||
| + | Una sonda espacial, considerada como un punto material <math>P\,</math> de masa <math>m\,</math>, se mueve en el plano OXY (descrito mediante las coordenadas polares <math>\rho\,</math> y <math>\theta\,</math> de la figura) cuyo origen <math>O\,</math> coincide con el centro de un planeta de radio <math>R\,</math>. Éste ejerce sobre la sonda una fuerza de atracción gravitatoria conservativa, cuya | ||
| + | energía potencial asociada viene dada por la expresión: | ||
| + | |||
| + | <center><math> | ||
| + | U(\rho)=-\frac{\gamma m}{\rho} \;\;\;\;\;\;\;\;\;\;\;\; \mathrm{(}\gamma\,\,\mathrm{es}\,\,\mathrm{una}\,\,\mathrm{constante}\,\, \mathrm{conocida)} | ||
| + | </math></center> | ||
| + | |||
| + | Mediante la acción de sus motores, la sonda es puesta en órbita desde la superficie del planeta siguiendo la espiral logarítmica de | ||
| + | ecuaciones horarias: | ||
| + | |||
| + | <center><math> | ||
| + | \rho(t)=R\, e^{\lambda\omega t}\,\, ; \,\,\,\,\,\,\,\,\,\,\,\,\,\,\theta(t)=\omega t\;\;\;\;\;\;\;\;\;\;\;\; \mathrm{(}\lambda\,\,\mathrm{y}\,\,\omega\,\,\mathrm{son}\,\,\mathrm{constantes}\,\,\mathrm{conocidas)} | ||
| + | </math></center> | ||
| + | |||
| + | Despreciando las posibles fuerzas de fricción sobre la sonda, así como las pérdidas de masa asociadas al gasto de combustible, se pide: | ||
| + | |||
| + | # Deducir razonadamente si el movimiento de la sonda es o no es un movimiento central con centro en <math>O\,</math>. | ||
| + | # Comprobar que la energía cinética de la sonda responde a la expresión <math>K=C\rho^2\,</math>, determinando el valor de la constante <math>C\,</math> en función de las constantes conocidas del problema. | ||
| + | # Aplicando el teorema de la energía, determinar el trabajo (no conservativo) realizado por los motores sobre la sonda durante el intervalo de tiempo que tarda ésta en duplicar su distancia inicial al centro del planeta. | ||
Revisión de 20:16 25 oct 2012
Enunciado
Una sonda espacial, considerada como un punto material 
de masa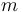 
, se mueve en el plano OXY (descrito mediante las coordenadas polares 
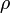y 
de la figura) cuyo origen 
coincide con el centro de un planeta de radio 
. Éste ejerce sobre la sonda una fuerza de atracción gravitatoria conservativa, cuya
energía potencial asociada viene dada por la expresión:
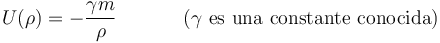
Mediante la acción de sus motores, la sonda es puesta en órbita desde la superficie del planeta siguiendo la espiral logarítmica de ecuaciones horarias:
Despreciando las posibles fuerzas de fricción sobre la sonda, así como las pérdidas de masa asociadas al gasto de combustible, se pide:
- Deducir razonadamente si el movimiento de la sonda es o no es un movimiento central con centro en .
- Comprobar que la energía cinética de la sonda responde a la expresión
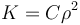, determinando el valor de la constante 
en función de las constantes conocidas del problema.
- Aplicando el teorema de la energía, determinar el trabajo (no conservativo) realizado por los motores sobre la sonda durante el intervalo de tiempo que tarda ésta en duplicar su distancia inicial al centro del planeta.
