Rectas de mejor ajuste en Excel
De Laplace
(Página creada con '==Introducción== ==Que es una recta de mejor ajuste== ==Por qué se llama “de mínimos cuadrados”== ==Como se calcula== ===Pendiente=== ===Ordenada en el origen=== …') |
|||
| Línea 1: | Línea 1: | ||
==Introducción== | ==Introducción== | ||
| + | En la mayoría de las prácticas de laboratorio se requiere el trazado de una o varias “rectas de mejor ajuste” o “rectas de mínimos cuadrados” (en nuestro contexto, ambos términos son sinónimos). En este artículo se trata de explicar de froma lo más clara posible qué son, como se calculan y sobre todo, cómo se representan gráficamente de forma correcta. Aparte de las fórmulas, explicaremos el procedimiento particularizado en el programa Excel. | ||
| + | |||
==Que es una recta de mejor ajuste== | ==Que es una recta de mejor ajuste== | ||
| + | Muchas leyes físicas obedecen un comportamiento lineal, que quiere decir que una variable depende de otra como una función de primer grado. Así, por ejemplo, la ley de Hooke nos relaciona la fuerza aplicada a un muelle con la elongación de éste respecto a la posición de equilibrio) | ||
| + | |||
| + | <center><math>|\vec{F}| = k(l-l_\mathrm{eq})\qquad\Rightarrow\qquad l=l_\mathrm{eq}+\frac{|\vec{F}|}{k}</math></center> | ||
| + | |||
| + | Si esta fuerza la aplicamos colgando sucesivas masas, obtenemos la relación teórica | ||
| + | |||
| + | <center><math>l =l_\mathrm_{eq} + \frac{g}{k}m</math></center> | ||
| + | |||
| + | que es un caso particular de relación lineal | ||
| + | |||
| + | <center><math>l = a + b m\qquad\qquad a = l_\mathrm{eq}\qquad\qquad b = \frac{g}{k}</math></center> | ||
| + | |||
| + | donde <math>a</math> es la llamada ''ordenada en el origen'' y <math>b</math> es la ''pendiente''. | ||
| + | así que, idealmente, si representamos la elongación | ||
| + | |||
| + | |||
| + | Cuando se tienen dos puntos experimentales | ||
==Por qué se llama “de mínimos cuadrados”== | ==Por qué se llama “de mínimos cuadrados”== | ||
==Como se calcula== | ==Como se calcula== | ||
Revisión de 16:28 25 oct 2012
Contenido |
1 Introducción
En la mayoría de las prácticas de laboratorio se requiere el trazado de una o varias “rectas de mejor ajuste” o “rectas de mínimos cuadrados” (en nuestro contexto, ambos términos son sinónimos). En este artículo se trata de explicar de froma lo más clara posible qué son, como se calculan y sobre todo, cómo se representan gráficamente de forma correcta. Aparte de las fórmulas, explicaremos el procedimiento particularizado en el programa Excel.
2 Que es una recta de mejor ajuste
Muchas leyes físicas obedecen un comportamiento lineal, que quiere decir que una variable depende de otra como una función de primer grado. Así, por ejemplo, la ley de Hooke nos relaciona la fuerza aplicada a un muelle con la elongación de éste respecto a la posición de equilibrio)
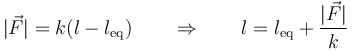
Si esta fuerza la aplicamos colgando sucesivas masas, obtenemos la relación teórica
que es un caso particular de relación lineal
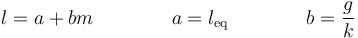
donde a es la llamada ordenada en el origen y b es la pendiente. así que, idealmente, si representamos la elongación
Cuando se tienen dos puntos experimentales





