Velocidad media en un movimiento armónico
De Laplace
(Página creada con '==Enunciado== Una partícula describe un movimiento armónico simple de frecuencia angular <math>\omega</math>, pudiéndose mover a lo largo de una recta horizontal. En <math>t=…') |
|||
| Línea 10: | Línea 10: | ||
<center><math>v_m = \frac{\Delta x}{\Delta t}</math></center> | <center><math>v_m = \frac{\Delta x}{\Delta t}</math></center> | ||
| + | En este caso, el intervalo se nos da como dato: es la cuarta parte del periodo | ||
| + | |||
| + | <center><math>\Delta t = \frac{T}{4}</math></center> | ||
| + | |||
| + | En un movimiento armónico simple, una partícula que parte del punto de equilibrio en <math>t=0</math> alcanza la máxima elongación en <math>T/4</math>; en <math>T/2</math> vuelve a pasar por el origen en <math>3T/4</math> alcanza la distancia máxima por el lado opuesto y en <math>T</math> regresa al origen, completando el ciclo. | ||
| + | |||
| + | <center>[[Archivo:xt-mas.png]]</center> | ||
| + | |||
| + | Por tanto el desplazamiento entre <math>t=0</math> y <math>t=T/4</math> es igual a la elongación máxima, es decir a la amplitud. | ||
| + | |||
| + | <center><math>\Delta x = A</math></center> | ||
==Aceleración== | ==Aceleración== | ||
[[Categoría:Problemas de cinemática del movimiento rectilíneo (GIE)]] | [[Categoría:Problemas de cinemática del movimiento rectilíneo (GIE)]] | ||
Revisión de 17:40 18 oct 2012
1 Enunciado
Una partícula describe un movimiento armónico simple de frecuencia angular ω, pudiéndose mover a lo largo de una recta horizontal. En t = 0 pasa por la posición de equilibrio con una velocidad + v0.
- ¿Cuánto vale la velocidad media entre t = 0 y t = T / 4, con T el periodo de oscilación?
- ¿Cuánto vale la aceleración en t = T / 4?
2 Velocidad media
La velocidad media de una partícula en un movimiento rectilíneo se calcula como el cociente entre el desplazamiento neto y la duración del intervalo en que se realiza
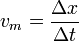
En este caso, el intervalo se nos da como dato: es la cuarta parte del periodo
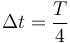
En un movimiento armónico simple, una partícula que parte del punto de equilibrio en t = 0 alcanza la máxima elongación en T / 4; en T / 2 vuelve a pasar por el origen en 3T / 4 alcanza la distancia máxima por el lado opuesto y en T regresa al origen, completando el ciclo.
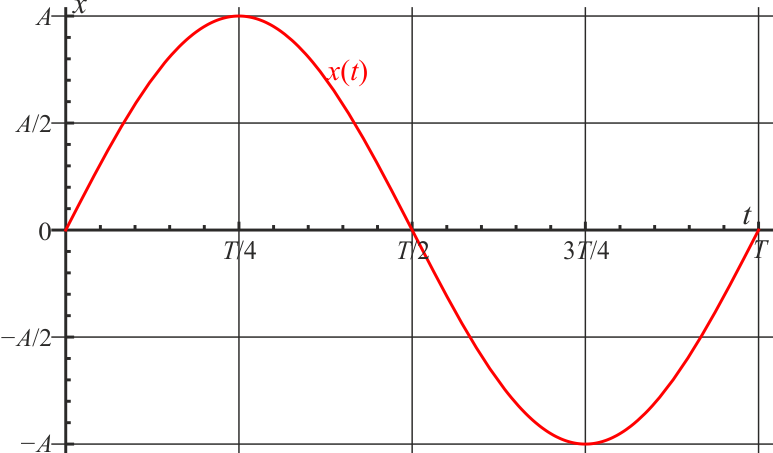
Por tanto el desplazamiento entre t = 0 y t = T / 4 es igual a la elongación máxima, es decir a la amplitud.





