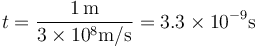Entrar Página Discusión Historial Go to the site toolbox

Ejemplos de órdenes de magnitud

De Laplace

(Diferencias entre revisiones)
(→Longitudes)
(→Tiempos)
 
(14 ediciones intermedias no se muestran.)
Línea 61: Línea 61:
:es decir la estrella más cercana está a una distancia del orden de 10<sup>16</sup>m.
:es decir la estrella más cercana está a una distancia del orden de 10<sup>16</sup>m.
-
Cuando se
+
Tabulando estos resultados, nos queda
 +
 
 +
{| class="bordeado"
 +
|-
 +
! Sistema
 +
! Orden de magnitud (m)
 +
|-
 +
| Núcleo atómico
 +
| 10<sup>&minus;15</sup>
 +
|-
 +
| Átomo
 +
| 10<sup>&minus;10</sup>
 +
|-
 +
| Bacteria
 +
| 10<sup>&minus;5</sup> &ndash; 10<sup>&minus;6</sup>
 +
|-
 +
| Espesor de un folio
 +
| 10<sup>&minus;4</sup>
 +
|-
 +
| Ser humano
 +
| 10<sup>0</sup>
 +
|-
 +
| Altura a la que se encuentra la ISS
 +
| 10<sup>5</sup>
 +
|-
 +
| España
 +
| 10<sup>6</sup>
 +
|-
 +
| Circunferencia terrestre
 +
| 10<sup>7</sup>
 +
|-
 +
| Distancia Tierra-Sol
 +
| 10<sup>11</sup>
 +
|-
 +
| Distancia a &alpha;-Centauri
 +
| 10<sup>16</sup>
 +
|}
==Masas==
==Masas==
 +
Seguimos el mismo procedimiento de ordenar en primer lugar sin dar valores.
 +
 +
# Núcleo atómico
 +
# Bacteria
 +
# Hormiga
 +
# Folio
 +
# Ser humano
 +
# Elefante adulto
 +
# Agua de una piscina olímpica
 +
# Montaña más alta
 +
# Tierra
 +
# Sol
 +
 +
Ahora comenzamos a asignar valores:
 +
 +
* La masa de un ser humano se encuentra en el orden de magnitud de 100kg.
 +
* Un folio es una lámina de papel cuyas dimensiones (en un A4) son de 210mm&times;297mm y cuyo espesor, según hemos comentado, es de aproximadamente 0.1mm. Esto nos da un volumen
 +
 +
<center><math>V = 210\times 297\times 0.1\,\mathrm{mm}^3 = 6237\,\mathrm{mm}^3 \sim 10^{-5} - 10^{-6}\,\mathrm{m}^3</math></center>
 +
 +
:La densidad del papel es algo menor a la del agua (está hecho de celulosa, como la madera), es decir, ronda los 1000kg/m&sup3; por lo que su masa es del orden
 +
 +
<center><math>m\sim 10^{-2}---10^{-3}\,\mathrm{kg}</math></center>
 +
 +
:es decir, pesa algunos gramos. A este valor se puede llegar de muchas otras formas. Por ejemplo, la densidad superficial de un folio suele ser 80g/m&sup2;, lo que nos da una masa
 +
 +
<center><math>m \simeq (0.210\,\mathrm{m})\times (0.297\,\mathrm{m})\times 80\frac{\mathrm{g}}{\mathrm{m}^2}\times \frac{1\,\mathrm{kg}}{1000\,\mathrm{g}} = 5\times 10^{-3}\,\mathrm{kg}</math></center>
 +
 +
:o bien, podemos observar que un paquete de 500 folios pesa más de 2kg.
 +
 +
* Para una hormiga el cálculo es parecido. Su volumen viene a ser 1mm&sup3; y su densidad es muy parecida a la del agua (como en todos los seres vivos), lo que nos da una masa de unos 10<sup>&minus;6</sup>kg (del orden de 1mg).
 +
 +
* Igualmente con una bacteria, cuyo diámetro viene a ser entre 1 y 10 micras (10<sup>&minus;5</sup>m &ndash; 10<sup>&minus;6</sup>m ). Para 10 micras nos da una masa
 +
 +
<center><math>m \sim (10^{-5})^3\times 1000\,\mathrm{kg} = 10^{-12}\,\mathrm{kg}</math></center>
 +
 +
:es decir, 1ng. Para 1 micra sale 1000 veces menos, esto es, 1pg.
 +
 +
* Un núcleo atómico es una agrupación de unos cuantos protones y neutrones (1 en el caso del hidrógeno y más de 200 en el uranio y más allá). La masa de un protón y un neutrón es muy parecida y aproximadamente igual a 1.6\times 10<sup>&minus;27</sup>kg, lo que nos da una masa en el rango
 +
 +
<center><math>m \sim 10^{-27} - 10^{-25}\,\mathrm{kg}</math></center>
 +
 +
* Por encima del ser humano, tenemos en primer lugar a un elefante, cuyo masa dependerá del ejemplar, pero que puede llegar hasta las 10 toneladas (10<sup>4</sup>kg)
 +
 +
* Una piscina olímpica mide de largo 50m. El ancho podrá variar, pero si Phelps puede nadar mariposa con comodidad, el ancho de una calle debe ser más de 2m. Puesto que hay 8 calles, el ancho ronda los 20m. La profundidad es variable, pero entre 2m y 3m es un valor típico. Esto nos da la masa
 +
 +
<center><math>m \sim 50\,\mathrm{m}\times 20\,\mathrm{m}\times 3\,\mathrm{m}\times 1000\,\frac{\mathrm{kg}}{\mathrm{m}^3} \sim 3\times 10^6\,\mathrm{kg}</math></center>
 +
 +
* La cuestión de la montaña es la más peliaguda, pues depende de cómo definamos la montaña. Todos tenemos claro hasta donde llega, pero, ¿desde donde se empieza a contar? ¿Desde el nivel del mar? ¿desde el centro de la Tierra? ¿desde la base de la montaña? Según el criterio que se emplee la montaña tiene una altura diferente. Así, por ejemplo, el Everest mide 8848m desde el nivel del mar, pero si contamos que el Himalaya se encuentra sobre la meseta del Tibet, su altura no llega a los 4000m. A la inversa, el volcán Mauna Kea se eleva solo 4205m sobre el nivel del mar, pero contando desde su base es más alto que el Everest, con 10200m. Para hallar el orden de magnitud, suponemos en ambos casos una altura del orden de 10km. ¿Y que anchura le colocamos? Siguiendo el ejemplo del Mauna kea, se trata de un cono, cuyo radio es similar a su altura. Esto nos da un volumen (aplicando la fórmula para un cono)
 +
 +
<center><math>V = \frac{1}{3}\pi R^2 h \sim 10\,\mathrm{km}^3</math></center>
 +
 +
:La densidad de masa de la roca es de 3 o 4 veces la del agua, lo que nos da una masa
 +
 +
<center><math>m \sim (10^4)^3\times 10^3\,\mathrm{kg} = 10^{15}\mathrm{kg}</math></center>
 +
 +
* La Tierra es una esfera de roca con radio de 6370\,km y volumen
 +
 +
<center><math>V = \frac{4\pi}{3}R^3 = \frac{4\pi}{3}(6.37\times 10^6)^3\,\mathrm{m}^3 \simeq 10^{21}\mathrm{m}^3</math></center>
 +
 +
: La densidad de la roca en la corteza es 3 o 4 veces la del agua; en las profundidades es más densa pero eso no cambia mucho el orden de magnitud. Esto nos da una masa
 +
 +
<center><math>m \sim 10^21\,\mathrm{m}^3\times 10^4\,\frac{\mathrm{kg}}{\mathrm{m}^3} \sim 10^{25}\,\mathrm{kg}</math></center>
 +
 +
: Podemos pesar la Tierra empleando la ley de la gravitación universal. La aceleración de la gravedad es igual al campo gravitatorio en la superficie de la Tierra
 +
 +
<center><math>g = \frac{GM_T}{R_T^2} \qquad\Rightarrow\qquad M_T = \frac{g R^2}{G} = \frac{9.81\times (6.37\times 10^6)^2}{6.67\times 10^{-11}}\,\mathrm{kg} \simeq 6\times 10^24\,\mathrm{kg}</math></center>
 +
 +
* Por último, para el Sol, su masa puede determinarse también a partir de la ley de Newton de la gravitación universal. El resultado al que se llega así es
 +
 +
<center><math>m \sim 10^{33}\,\mathrm{kg}</math></center>
 +
 +
{| class="bordeado"
 +
|-
 +
! Sistema
 +
! Orden de magnitud (kg)
 +
|-
 +
| Núcleo atómico
 +
| 10<sup>&minus;25</sup> &ndash; 10<sup>&minus;27</sup>
 +
|-
 +
| Bacteria
 +
| 10<sup>&minus;12</sup> &ndash; 10<sup>&minus;15</sup>
 +
|-
 +
| Hormiga
 +
| 10<sup>&minus;6</sup>
 +
|-
 +
| Folio
 +
| 10<sup>&minus;2</sup>
 +
|-
 +
| Ser humano
 +
| 10<sup>2</sup>
 +
|-
 +
| Elefante adulto
 +
| 10<sup>4</sup>
 +
|-
 +
| Piscina olímpica
 +
| 10<sup>6</sup>
 +
|-
 +
| Montaña
 +
| 10<sup>15</sup>
 +
|-
 +
| Tierra
 +
| 10<sup>25</sup>
 +
|-
 +
| Sol
 +
| 10<sup>33</sup>
 +
|}
 +
==Tiempos==
==Tiempos==
 +
En primer lugar, ordenamos de menor a mayor:
 +
 +
# Tiempo que la luz tarda en recorrer 1&thinsp;m
 +
# Consulta a un disco duro
 +
# Aleteo de un colibrí
 +
# Parpadeo
 +
# Latido de un corazón
 +
# Día
 +
# Año
 +
# Vida humana
 +
# Civilización
 +
# Edad de la Tierra
 +
 +
En este caso, hay varios que pueden presentar dudas: ¿qué es más rápido, un latido o un parpadeo? ¿Cuál es la frecuencia de aleto de un colibrí? En muchos casos, una consulta a la wikipedia resuelve nuestras dudas.
 +
 +
Empezamos por lo más fácil:
 +
 +
* Un día tiene
 +
 +
<center><math>t = 24\,\mathrm{h}\times \frac{60\,\mathrm{min}}{1\,\mathrm{h}}\times \frac{60\,\mathrm{s}}{1\,\mathrm{min}} = 86400\,\mathrm{s}\sim 10^5\,\mathrm{s}</math></center>
 +
 +
* Un año son 365 días, luego
 +
 +
<center><math>t \sim 10^7\,\mathrm{s}</math></center>
 +
 +
* Una vida humana promedio es del orden de magnitud de 100 años
 +
 +
<center><math>t\sim 10^9\,\mathrm{s}</math></center>
 +
 +
* La civilización humana (que no la especie humana) se puede contabilizar desde la invención de la agricultura y los primeros escritos (o un poco antes, pero dentro del mismo orden de magnitud). Eso son unos 10000 años
 +
 +
<center><math>t\sim 10^{11}\,\mathrm{s}</math></center>
 +
 +
* La Tierra es bastante más antigua (si uno no es creacionista, claro). Tiene unos 4500 millones de años
 +
 +
<center><math>t \sim 10^9\times 10^7 = 10^{16}</math></center>
 +
 +
Un cálculo más preciso, teniendo encuenta que 365 días no son 100 días y que 4500 no son 1000 nos da un orden de magnitud más
 +
 +
<center><math>t\sim 10^{17}\,\mathrm{s}</math></center>
 +
 +
* El latido del corazon lo hallamos observando que un ritmo cardiaco normal es del orden de 60 latidos por minuto, luego
 +
 +
<center><math>t\sim 1\,\mathrm{s}</math></center>
 +
 +
* Un parpadeo, en cambio, es sin duda más corto que un latido (no se tarda un segundo en parpadear). Ronda más bien la décima de sgundo
 +
 +
<center><math>t\sim 10^{-1}\,\mathrm{s}</math></center>
 +
 +
* Un [http://es.wikipedia.org/wiki/Colibri colibrí] puede aletear hasta 60 o 70 veces por segundo, lo que nos da un tiempo por cada aleteo
 +
 +
<center><math>t \sim 10^{-2}\mathrm{s}</math></center>
 +
 +
* Una consulta a un disco duro es el tiempo que se tarda en leer un dato de éste. Puede variar bastante, pero sabemos que es muy rápido, mucho más que el aleteo de un colibrí. Ronda el milisegundo
 +
 +
<center><math>t \sim 10^{-3}\mathrm{s}</math></center>
 +
 +
* La luz tarda un tiempo muy corto en recorrer un metro, concretamente
 +
 +
<center><math>t = \frac{1\,\mathrm{m}}{3\times 10^8\mathrm{m}/\mathrm{s}} = 3.3\times 10^{-9}\mathrm{s}</math></center>
 +
 +
[[Categoría:Problemas de introducción a la física (GIE)]]
[[Categoría:Problemas de introducción a la física (GIE)]]

última version al 14:08 28 sep 2012

Contenido

1 Enunciado

Indique valores para los ordenes de magnitud de las siguientes longitudes, masas o tiempos, en el SI.

Longitudes

1. Bacteria — 2. Ser humano — 3. Distancia Tierra-Sol — 4. Circunferencia terrestre — 5. Átomo — 6. España — 7. Espesor de un folio — 8. Distancia a α-Centauri — 9. Núcleo atómico — 10. Altura a la que se encuentra la ISS

Masas

1. Bacteria — 2. Ser humano — 3. Tierra — 4. Hormiga — 5. Sol — 6. Montaña más alta — 7. Folio — 8. Agua de una piscina olímpica — 9. Núcleo atómico — 10. Elefante adulto

Tiempos

1. Día — 2. Año — 3. Vida humana — 4. Latido de un corazón — 5. Tiempo que la luz tarda en recorrer 1 m — 6. Edad de la Tierra — 7. Parpadeo — 8. Aleteo de un colibrí — 9. Consulta a un disco duro — 10. Civilización

2 Longitudes

Comenzamos ordenándolos de menor a mayor. Es fácil ver que queda

  1. Núcleo atómico
  2. Átomo
  3. Bacteria
  4. Espesor de un folio
  5. Ser humano
  6. Altura a la que se encuentra la ISS
  7. España
  8. Circunferencia terrestre
  9. Distancia Tierra-Sol
  10. Distancia a α-Centauri

Quizás la única duda es la altura a la que se encuentra la ISS. Esta es la Estación Espacial Internacional. En un satélite artificial que se encuentra en órbita alrededor de la Tierra. Podría pensarse que se halla en el espacio exterior, a distancias comparables a la distancia Tierra-Sol, pèro en realidad se halla a baja altura, de unos 500km, por lo que esta altura es incluso menor que el tamaño de España (1000km).

A continuación estimamos órdenes de magnitud.

  • Para el cuerpo humano, las distancias son del orden de 1 m (eso no quiere decir que un ser humano mida aproximadamente 1 m, sino que es de ese orden de magnitud).

Yendo hacia distancias menores

  • Tenemos que un folio mide del orden de una décima de milímetro, luego su orden de magnitud es 10−4m. A este valor se llega observando que, por ejemplo, un paquete de 500 folios mide unos 5cm de espesor.
  • Bacterias hay de muchos tamaños, pero los típicos pueden estar entre 1 y 10 micras, es decir entre 10−5m y 10−6m.
  • Un átomo es del orden de 10−10m (lo que se llama un Angstrom, aunque esta unidad está en desuso).
  • Un núcleo atómico es muchísimo más pequeño que un átomo. Su diámetro puede rondar los 10−15m, es decir es una cienmilésima del radio del átomo completo.

Yendo hacia arriba,

  • La ISS está a una altura de unos cientos de km, esto es, 105m.
  • España mide unos 1000km (sin contar Canarias), lo que da su tamaño típico 106m
  • El metro se definió originalmente como la diezmillónesima parte de un cuarto de circunferencia terrestre, por lo que esta vale 40000km, es decir, está en el orden de 107m
  • La distancia media Tierra-Sol (lo que se conoce como Unidad Astronómica) es de 150 millones de kilómetros, lo que corresponde 1011m.
  • α Centauri es la estrella (en realidad una estrella doble) más cercana al Sol, y aun así su distancia es de 4.6 años luz, siendo un año luz
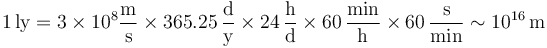
1\,\mathrm{ly} = 3\times 10^8\frac{\mathrm{m}}{\mathrm{s}}\times 365.25\,\frac{\mathrm{d}}{\mathrm{y}}\times 24\,\frac{\mathrm{h}}{\mathrm{d}}\times 60\,\frac{\mathrm{min}}{\mathrm{h}}\times 60\,\frac{\mathrm{s}}{\mathrm{min}}\sim 10^{16}\,\mathrm{m}
es decir la estrella más cercana está a una distancia del orden de 1016m.

Tabulando estos resultados, nos queda

Sistema Orden de magnitud (m)
Núcleo atómico 10−15
Átomo 10−10
Bacteria 10−5 – 10−6
Espesor de un folio 10−4
Ser humano 100
Altura a la que se encuentra la ISS 105
España 106
Circunferencia terrestre 107
Distancia Tierra-Sol 1011
Distancia a α-Centauri 1016

3 Masas

Seguimos el mismo procedimiento de ordenar en primer lugar sin dar valores.

  1. Núcleo atómico
  2. Bacteria
  3. Hormiga
  4. Folio
  5. Ser humano
  6. Elefante adulto
  7. Agua de una piscina olímpica
  8. Montaña más alta
  9. Tierra
  10. Sol

Ahora comenzamos a asignar valores:

  • La masa de un ser humano se encuentra en el orden de magnitud de 100kg.
  • Un folio es una lámina de papel cuyas dimensiones (en un A4) son de 210mm×297mm y cuyo espesor, según hemos comentado, es de aproximadamente 0.1mm. Esto nos da un volumen
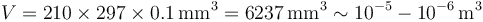
V = 210\times 297\times 0.1\,\mathrm{mm}^3 = 6237\,\mathrm{mm}^3 \sim 10^{-5} - 10^{-6}\,\mathrm{m}^3
La densidad del papel es algo menor a la del agua (está hecho de celulosa, como la madera), es decir, ronda los 1000kg/m³ por lo que su masa es del orden
m\sim 10^{-2}---10^{-3}\,\mathrm{kg}
es decir, pesa algunos gramos. A este valor se puede llegar de muchas otras formas. Por ejemplo, la densidad superficial de un folio suele ser 80g/m², lo que nos da una masa
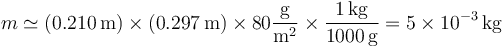
m \simeq (0.210\,\mathrm{m})\times (0.297\,\mathrm{m})\times 80\frac{\mathrm{g}}{\mathrm{m}^2}\times \frac{1\,\mathrm{kg}}{1000\,\mathrm{g}} = 5\times 10^{-3}\,\mathrm{kg}
o bien, podemos observar que un paquete de 500 folios pesa más de 2kg.
  • Para una hormiga el cálculo es parecido. Su volumen viene a ser 1mm³ y su densidad es muy parecida a la del agua (como en todos los seres vivos), lo que nos da una masa de unos 10−6kg (del orden de 1mg).
  • Igualmente con una bacteria, cuyo diámetro viene a ser entre 1 y 10 micras (10−5m – 10−6m ). Para 10 micras nos da una masa
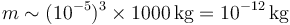
m \sim (10^{-5})^3\times 1000\,\mathrm{kg} = 10^{-12}\,\mathrm{kg}
es decir, 1ng. Para 1 micra sale 1000 veces menos, esto es, 1pg.
  • Un núcleo atómico es una agrupación de unos cuantos protones y neutrones (1 en el caso del hidrógeno y más de 200 en el uranio y más allá). La masa de un protón y un neutrón es muy parecida y aproximadamente igual a 1.6\times 10−27kg, lo que nos da una masa en el rango
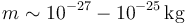
m \sim 10^{-27} - 10^{-25}\,\mathrm{kg}
  • Por encima del ser humano, tenemos en primer lugar a un elefante, cuyo masa dependerá del ejemplar, pero que puede llegar hasta las 10 toneladas (104kg)
  • Una piscina olímpica mide de largo 50m. El ancho podrá variar, pero si Phelps puede nadar mariposa con comodidad, el ancho de una calle debe ser más de 2m. Puesto que hay 8 calles, el ancho ronda los 20m. La profundidad es variable, pero entre 2m y 3m es un valor típico. Esto nos da la masa
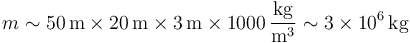
m \sim 50\,\mathrm{m}\times 20\,\mathrm{m}\times 3\,\mathrm{m}\times 1000\,\frac{\mathrm{kg}}{\mathrm{m}^3} \sim 3\times 10^6\,\mathrm{kg}
  • La cuestión de la montaña es la más peliaguda, pues depende de cómo definamos la montaña. Todos tenemos claro hasta donde llega, pero, ¿desde donde se empieza a contar? ¿Desde el nivel del mar? ¿desde el centro de la Tierra? ¿desde la base de la montaña? Según el criterio que se emplee la montaña tiene una altura diferente. Así, por ejemplo, el Everest mide 8848m desde el nivel del mar, pero si contamos que el Himalaya se encuentra sobre la meseta del Tibet, su altura no llega a los 4000m. A la inversa, el volcán Mauna Kea se eleva solo 4205m sobre el nivel del mar, pero contando desde su base es más alto que el Everest, con 10200m. Para hallar el orden de magnitud, suponemos en ambos casos una altura del orden de 10km. ¿Y que anchura le colocamos? Siguiendo el ejemplo del Mauna kea, se trata de un cono, cuyo radio es similar a su altura. Esto nos da un volumen (aplicando la fórmula para un cono)
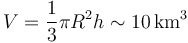
V = \frac{1}{3}\pi R^2 h \sim 10\,\mathrm{km}^3
La densidad de masa de la roca es de 3 o 4 veces la del agua, lo que nos da una masa
m \sim (10^4)^3\times 10^3\,\mathrm{kg} = 10^{15}\mathrm{kg}
  • La Tierra es una esfera de roca con radio de 6370\,km y volumen
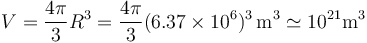
V = \frac{4\pi}{3}R^3 = \frac{4\pi}{3}(6.37\times 10^6)^3\,\mathrm{m}^3 \simeq 10^{21}\mathrm{m}^3
La densidad de la roca en la corteza es 3 o 4 veces la del agua; en las profundidades es más densa pero eso no cambia mucho el orden de magnitud. Esto nos da una masa
m \sim 10^21\,\mathrm{m}^3\times 10^4\,\frac{\mathrm{kg}}{\mathrm{m}^3} \sim 10^{25}\,\mathrm{kg}
Podemos pesar la Tierra empleando la ley de la gravitación universal. La aceleración de la gravedad es igual al campo gravitatorio en la superficie de la Tierra
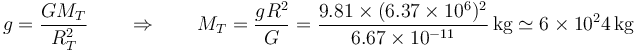
g = \frac{GM_T}{R_T^2} \qquad\Rightarrow\qquad M_T = \frac{g R^2}{G} = \frac{9.81\times (6.37\times 10^6)^2}{6.67\times 10^{-11}}\,\mathrm{kg} \simeq 6\times 10^24\,\mathrm{kg}
  • Por último, para el Sol, su masa puede determinarse también a partir de la ley de Newton de la gravitación universal. El resultado al que se llega así es
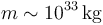
m \sim 10^{33}\,\mathrm{kg}
Sistema Orden de magnitud (kg)
Núcleo atómico 10−25 – 10−27
Bacteria 10−12 – 10−15
Hormiga 10−6
Folio 10−2
Ser humano 102
Elefante adulto 104
Piscina olímpica 106
Montaña 1015
Tierra 1025
Sol 1033

4 Tiempos

En primer lugar, ordenamos de menor a mayor:

  1. Tiempo que la luz tarda en recorrer 1 m
  2. Consulta a un disco duro
  3. Aleteo de un colibrí
  4. Parpadeo
  5. Latido de un corazón
  6. Día
  7. Año
  8. Vida humana
  9. Civilización
  10. Edad de la Tierra

En este caso, hay varios que pueden presentar dudas: ¿qué es más rápido, un latido o un parpadeo? ¿Cuál es la frecuencia de aleto de un colibrí? En muchos casos, una consulta a la wikipedia resuelve nuestras dudas.

Empezamos por lo más fácil:

  • Un día tiene
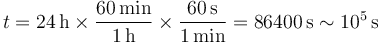
t = 24\,\mathrm{h}\times \frac{60\,\mathrm{min}}{1\,\mathrm{h}}\times \frac{60\,\mathrm{s}}{1\,\mathrm{min}} = 86400\,\mathrm{s}\sim 10^5\,\mathrm{s}
  • Un año son 365 días, luego
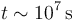
t \sim 10^7\,\mathrm{s}
  • Una vida humana promedio es del orden de magnitud de 100 años
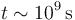
t\sim 10^9\,\mathrm{s}
  • La civilización humana (que no la especie humana) se puede contabilizar desde la invención de la agricultura y los primeros escritos (o un poco antes, pero dentro del mismo orden de magnitud). Eso son unos 10000 años
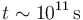
t\sim 10^{11}\,\mathrm{s}
  • La Tierra es bastante más antigua (si uno no es creacionista, claro). Tiene unos 4500 millones de años
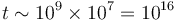
t \sim 10^9\times 10^7 = 10^{16}

Un cálculo más preciso, teniendo encuenta que 365 días no son 100 días y que 4500 no son 1000 nos da un orden de magnitud más

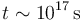
t\sim 10^{17}\,\mathrm{s}
  • El latido del corazon lo hallamos observando que un ritmo cardiaco normal es del orden de 60 latidos por minuto, luego
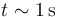
t\sim 1\,\mathrm{s}
  • Un parpadeo, en cambio, es sin duda más corto que un latido (no se tarda un segundo en parpadear). Ronda más bien la décima de sgundo
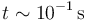
t\sim 10^{-1}\,\mathrm{s}
  • Un colibrí puede aletear hasta 60 o 70 veces por segundo, lo que nos da un tiempo por cada aleteo
t˜10 − 2s
  • Una consulta a un disco duro es el tiempo que se tarda en leer un dato de éste. Puede variar bastante, pero sabemos que es muy rápido, mucho más que el aleteo de un colibrí. Ronda el milisegundo
t˜10 − 3s
  • La luz tarda un tiempo muy corto en recorrer un metro, concretamente
t = \frac{1\,\mathrm{m}}{3\times 10^8\mathrm{m}/\mathrm{s}} = 3.3\times 10^{-9}\mathrm{s}
Obtenido de "http://tesla.us.es/wiki/index.php/Ejemplos_de_%C3%B3rdenes_de_magnitud"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 14:08, 28 sep 2012. - Esta página ha sido visitada 50.650 veces. - Aviso legal - Acerca de Laplace