Gradiente
De Laplace
(Nueva página: ==Definición== ==Propiedades== ==Componentes en una base== ==Ejemplos== Categoría:Gradiente) |
(→Definición) |
||
| Línea 1: | Línea 1: | ||
==Definición== | ==Definición== | ||
| + | De la definición de [[derivada direccional]] resulta que dado un campo escalar, continuo y derivable, para cada punto del espacio existen infinitas derivadas direccionales, una por cada dirección. Resulta además que el concepto de derivada direccional depende tanto del campo escalar como de la dirección elegida. | ||
| + | |||
| + | ¿Existe alguna cantidad, independiente de la dirección, que permita calcular las derivadas direccionales, sin necesidad de hallar infinitas cantidades para cada punto. | ||
| + | |||
| + | La respuesta la da el ''gradiente'': Para un campo escalar <math>\phi\,</math> y un punto <math>P</math>, el gradiente <math>\nabla\phi</math> del campo en dicho punto es el ''único'' vector, dependiente exclusivamente del campo, tal que para cualquier dirección <math>\mathbf{v}</math>, la derivada direccional de <math>\phi\,</math> en <math>P</math> viene dada por el producto escalar | ||
| + | |||
| + | <center><math>\frac{\partial \phi}{\partial v} = \nabla\phi\cdot \mathbf{v}</math></center> | ||
| + | |||
| + | Equivalentemente, el gradiente puede definirse como el único vector tal que para cualquier desplazamiento diferencial \mathrm{d}\mathbf{r}, el incremento diferencial de <math>\phi\,</math> vale | ||
| + | |||
| + | <center><math>\mathrm{d}\phi = \nabla\phi\cdot\mathrm{d}\mathbf{r}</math></center> | ||
| + | |||
| + | No demostraremos que esta definición implica que dicho vector existe y además es único. | ||
| + | |||
==Propiedades== | ==Propiedades== | ||
==Componentes en una base== | ==Componentes en una base== | ||
==Ejemplos== | ==Ejemplos== | ||
[[Categoría:Gradiente]] | [[Categoría:Gradiente]] | ||
Revisión de 11:04 5 oct 2008
Contenido |
1 Definición
De la definición de derivada direccional resulta que dado un campo escalar, continuo y derivable, para cada punto del espacio existen infinitas derivadas direccionales, una por cada dirección. Resulta además que el concepto de derivada direccional depende tanto del campo escalar como de la dirección elegida.
¿Existe alguna cantidad, independiente de la dirección, que permita calcular las derivadas direccionales, sin necesidad de hallar infinitas cantidades para cada punto.
La respuesta la da el gradiente: Para un campo escalar 
y un punto P, el gradiente 
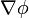del campo en dicho punto es el único vector, dependiente exclusivamente del campo, tal que para cualquier dirección 
, la derivada direccional de en P viene dada por el producto escalar
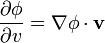
Equivalentemente, el gradiente puede definirse como el único vector tal que para cualquier desplazamiento diferencial \mathrm{d}\mathbf{r}, el incremento diferencial de vale
No demostraremos que esta definición implica que dicho vector existe y además es único.
