Entrar Página Discusión Historial Go to the site toolbox

Ejemplo de operaciones con dos vectores

De Laplace

(Diferencias entre revisiones)
 
Línea 56: Línea 56:
Por supuesto, también podíamos haber hallado esta parte simplemente restando del vector <math>\vec{a}</math>.
Por supuesto, también podíamos haber hallado esta parte simplemente restando del vector <math>\vec{a}</math>.
-
[[Categoría:Problemas de vectores libres (G.I.T.I.)]]
+
[[Categoría:Problemas de herramientas matemáticas (GIE)]]

última version al 11:34 19 sep 2012

Contenido

1 Enunciado

Dados los vectores

\vec{v}=2.0\vec{\imath}+3.5\vec{\jmath}-4.2\vec{k}\qquad\qquad\vec{a}=4.5\vec{\imath}-2.2\vec{\jmath}+1.5\vec{k}
  1. ¿Qué ángulo forman estos dos vectores?
  2. ¿Qué área tiene el paralelogramo que tiene a estos dos vectores por lados?
  3. Escriba \vec{a} como suma de dos vectores, uno paralelo a \vec{v} y otro ortogonal a él.

2 Ángulo

Obtenemos el ángulo a partir del producto escalar de los dos vectores

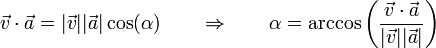
\vec{v}\cdot\vec{a}=|\vec{v}||\vec{a}|\cos(\alpha)\qquad\Rightarrow\qquad \alpha = \arccos\left(\frac{\vec{v}\cdot\vec{a}}{|\vec{v}||\vec{a}|}\right)

Tenemos que

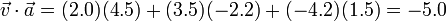
\vec{v}\cdot\vec{a}=(2.0)(4.5)+(3.5)(-2.2)+(-4.2)(1.5)=-5.0

y que

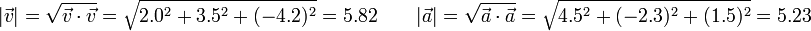
|\vec{v}| = \sqrt{\vec{v}\cdot\vec{v}}=\sqrt{2.0^2+3.5^2+(-4.2)^2} = 5.82\qquad |\vec{a}| = \sqrt{\vec{a}\cdot\vec{a}}=\sqrt{4.5^2+(-2.3)^2+(1.5)^2} = 5.23

lo que nos da

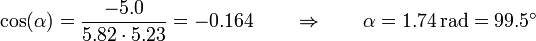
\cos(\alpha)=\frac{-5.0}{5.82\cdot 5.23}=-0.164\qquad\Rightarrow\qquad \alpha = 1.74\,\mathrm{rad}=99.5^\circ

3 Área

Podemos hallar el área a partir de lo que ya sabemos

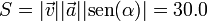
S = |\vec{v}||\vec{a}||\mathrm{sen}(\alpha)| = 30.0

o bien a partir del producto vectorial

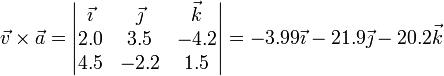
\vec{v}\times\vec{a}=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 2.0 & 3.5 & -4.2 \\ 4.5 & -2.2 & 1.5\end{matrix}\right| = -3.99\vec{\imath}-21.9\vec{\jmath} -20.2\vec{k}

cuyo módulo vale

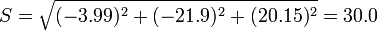
S = \sqrt{(-3.99)^2+(-21.9)^2+(20.15)^2} = 30.0

4 Descomposición

Para descomponer el vector \vec{a} aplicamos el doble producto vectorial para obtener

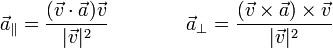
\vec{a}_\parallel = \frac{(\vec{v}\cdot\vec{a})\vec{v}}{|\vec{v}|^2}\qquad\qquad \vec{a}_\perp = \frac{(\vec{v}\times\vec{a})\times\vec{v}}{|\vec{v}|^2}

Conocemos aquí todas las cantidades salvo

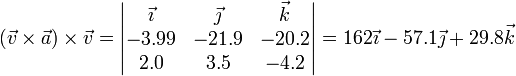
(\vec{v}\times\vec{a})\times\vec{v} = \left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ -3.99 & -21.9 & -20.2\\ 2.0 & 3.5 & -4.2 \end{matrix}\right| = 162\vec{\imath}-57.1\vec{\jmath} +29.8\vec{k}

Sustituyendo en las expresiones anteriores nos queda, para la parte paralela

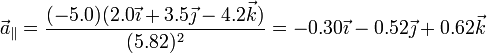
\vec{a}_\parallel = \frac{(-5.0)(2.0\vec{\imath}+3.5\vec{\jmath}-4.2\vec{k})}{(5.82)^2}=-0.30\vec{\imath}-0.52\vec{\jmath}+ 0.62\vec{k}

y para la normal

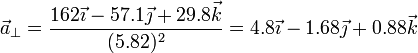
\vec{a}_\perp = \frac{162\vec{\imath}-57.1\vec{\jmath} +29.8\vec{k}}{(5.82)^2}=4.8\vec{\imath} -1.68\vec{\jmath}+ 0.88\vec{k}

Por supuesto, también podíamos haber hallado esta parte simplemente restando del vector \vec{a}.

Obtenido de "http://tesla.us.es/wiki/index.php/Ejemplo_de_operaciones_con_dos_vectores"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 11:34, 19 sep 2012. - Esta página ha sido visitada 3.695 veces. - Aviso legal - Acerca de Laplace