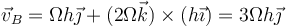Barra articulada rotatoria
De Laplace
(Página creada con '==Enunciado== Se tiene un sistema articulado formado por dos barras de la misma masa y la misma longitud <math>h</math> situadas sobre una superficie horizontal. La primera barr…') |
|||
| Línea 12: | Línea 12: | ||
==Velocidad de A y de B== | ==Velocidad de A y de B== | ||
===Velocidad de A=== | ===Velocidad de A=== | ||
| + | El punto A describe un movimiento de rotación alrededor de O, por lo que su velocidad cumple | ||
| + | |||
| + | <center><math>\vec{v}_A = \vec{\omega}\times\vec{r}_A</math></center> | ||
| + | |||
| + | siendo <math>\vec{r}_A</math> la posición respecto a O y <math>\vec{\omega}_1</math> la velocidad angular de la barra OA | ||
| + | |||
| + | <center><math>\vec{\omega}_1 = \Omega \vec{k}</math></center> | ||
| + | |||
| + | En el instante <math>t=0</math> las dos barras están completamente desplegadas y | ||
| + | |||
| + | <center><math>\vec{r}_A = \overrightarrow{OA}=\vec{h}\vec{\imath}</math></center> | ||
| + | |||
| + | lo que nos da la velocidad lineal de A | ||
| + | |||
| + | <center><math>\vec{v}_A =(\Omega \vec{k})\times (h\vec{\imath}) = \Omega h\vec{\jmath}</math></center> | ||
===Velocidad de B=== | ===Velocidad de B=== | ||
| + | El punto B también está rotando, pero no alrededor de O, sino alrededor del centro instantáneo de rotación, que localizaremos más adelante. Por ello, no podemoe emplear la misma fórmula que para A. En su lugar empleamos la fórmula general del campo de velocidades de un sólido | ||
| + | |||
| + | <center><math>\vec{v}_B = \vec{v}_A + \vec{\omega}_2\times\overrightarrow(AB}=\vec{v}_A + \vec{\omega}_2\times\left(\vec{r}_B-\vec{r}_A\right)</math></center> | ||
| + | |||
| + | donde <math>\vev{\omega}_2</math> es la velocidad angular de la segunda barra | ||
| + | |||
| + | <center><math>\vec{\omega}_2 = 2\Omega \vec{k}</math></center> | ||
| + | |||
| + | y <math>\vec{v}_A</math> es la velocidad lineal del punto A de la segunda barra. Al estar las dos barras articuladas en A, esta velocidad es la misma que la de la primera barra en A, que acabamos de calcular para <math>t=0</math> | ||
| + | |||
| + | <center><math>\vec{v}_A =(\Omega \vec{k})\times (h\vec{\imath}) = \Omega h\vec{\jmath}</math></center> | ||
| + | |||
| + | En este instante, la segunda barra se encuentra también desplegada | ||
| + | |||
| + | <center><math>\overrightarrow{AB}=\vec{r}_B-\vec{r}_A = h\vec{\jmath}</math></center> | ||
| + | |||
| + | lo que nos da la velocidad lineal de B en el instante <math>t=0</math> | ||
| + | |||
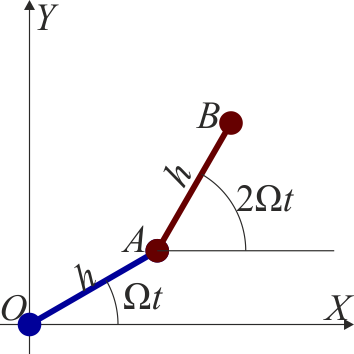
| + | <center><math>\vec{v}_B = \Omega h\vec{\jmath}+(2\Omega\vec{k})\times(h\vec{\imath}) = 3\Omega h\vec{\jmath}</math></center> | ||
| + | |||
| + | |||
==Posición del CIR== | ==Posición del CIR== | ||
==B en un instante posterior== | ==B en un instante posterior== | ||
Revisión de 21:08 7 sep 2012
Contenido |
1 Enunciado
Se tiene un sistema articulado formado por dos barras de la misma masa y la misma longitud h situadas sobre una superficie horizontal. La primera barra tiene un extremo O fijo, de forma que gira alrededor de él con velocidad angular constante Ω respecto a un sistema de ejes fijos OXY. La segunda barra está articulada en el extremo A de la primera y gira respecto de los mismos ejes fijos con una velocidad angular 2Ω. En el instante t = 0 el sistema está completamente extendido a lo largo del eje OX.
- Calcule la velocidad del punto de articulación A y del extremo libre B de la segunda barra en el instante t = 0.
- Localice la posición del centro instantáneo de rotación I del movimiento de la segunda barra respecto a los ejes fijos para el instante t = 0.
- Determine la posición del extremo B cuando ha pasado medio periodo, t = π / Ω, así como la velocidad de este punto en ese instante.
- Escriba las ecuaciones horarias de la posición del punto B para todo instante.
- Calcule la aceleración del extremo B de la barra en el instante t = 0. ¿Es nula alguna de sus componentes intrínsecas?
2 Velocidad de A y de B
2.1 Velocidad de A
El punto A describe un movimiento de rotación alrededor de O, por lo que su velocidad cumple
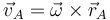
siendo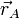 
la posición respecto a O y 
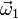la velocidad angular de la barra OA
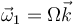
En el instante t = 0 las dos barras están completamente desplegadas y
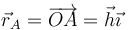
lo que nos da la velocidad lineal de A
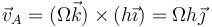
2.2 Velocidad de B
El punto B también está rotando, pero no alrededor de O, sino alrededor del centro instantáneo de rotación, que localizaremos más adelante. Por ello, no podemoe emplear la misma fórmula que para A. En su lugar empleamos la fórmula general del campo de velocidades de un sólido
donde No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \vev{\omega}_2
es la velocidad angular de la segunda barra
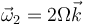
y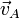 
es la velocidad lineal del punto A de la segunda barra. Al estar las dos barras articuladas en A, esta velocidad es la misma que la de la primera barra en A, que acabamos de calcular para t = 0
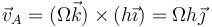
En este instante, la segunda barra se encuentra también desplegada
lo que nos da la velocidad lineal de B en el instante t = 0
