Propulsión con resorte
De Laplace
(→Enunciado) |
(→Contracción del muelle) |
||
| (6 ediciones intermedias no se muestran.) | |||
| Línea 11: | Línea 11: | ||
<center>[[Archivo:propulsion-resorte.png]]</center> | <center>[[Archivo:propulsion-resorte.png]]</center> | ||
| + | ==Velocidad del resorte== | ||
| + | La masa unida al resorte no experimenta fuerzas de rozamiento y está sometida exclusivamente a fuerzas conservativas y por tanto se conserva la energía mecánica. | ||
| + | |||
| + | <center><math>E = K + U = \mathrm{cte}\,</math></center> | ||
| + | |||
| + | La energía potencial es la suma de la gravitatoria (que es constante, por ser la superficie horizontal) y la elástica. Podemos ignorar la gravitatoria, pues siempre va a tener el mismo valor. Esto nos deja con la ley de conservación | ||
| + | |||
| + | <center><math>\frac{1}{2}m_1v^2 + \frac{1}{2}mv^2 = \mathrm{cte}</math></center> | ||
| + | |||
| + | Para hallar la velocidad de impacto, igualamos la energía mecánica en el momento de máxima compresión, con la que tiene la masa 1 en el momento del golpe. En el primer caso, la masa está instantáneamente en reposo y su energía cinética es nula, y en el segundo se halla en la posición de equilibrio, por lo que se anula su energía potencial. Esto nos da | ||
| + | |||
| + | <center><math>\frac{1}{2}kA^2 = \frac{1}{2}m_1v_1^2\qquad\Rightarrow\qquad v_1 = \sqrt{\frac{k}{m}}A</math></center> | ||
| + | |||
| + | Sustituyendo los valores numéricos | ||
| + | |||
| + | <center><math>v_1 = \sqrt{\frac{10}{0.1}}0.1\,\frac{\mathrm{m}}{\mathrm{s}} = 1.0\,\frac{\mathrm{m}}{\mathrm{s}}</math></center> | ||
| + | |||
| + | ==Velocidades tras la colisión== | ||
| + | Una vez que se produce la colisión tanto la masa unida al muelle, como la que se encuentra sobre el plano, tienen nuevas velocidades. Para hallarlas aplicamos la ley de conservación de la cantidad de movimiento | ||
| + | |||
| + | <center><math>m_1v_{1i}+m_2\overbrace{v_{2i}}^{=0} = m_1v_{1f}+m_2v_{2f}</math></center> | ||
| + | |||
| + | y que la colisión es perfectamente elástica, con lo que se conserva la energía cinética del sistema, o equivalentemente, el coeficiente de restitución es la unidad | ||
| + | |||
| + | <center><math>1 = \frac{v_{2f}-v_{1f}}{v_{1i}-v_{2i}}\qquad \Rightarrow\qquad v_{1i}-\overbrace{v_{2i}}^{=0} = v_{2f}-v_{1i}</math></center> | ||
| + | |||
| + | Resolviendo el sistema de dos ecuaciones con dos incógnitas queda | ||
| + | |||
| + | <center><math>v_{1f}=\frac{m_1-m_2}{m_1+m_2}v_{1i}=\frac{100-300}{100+300}\cdot 1.0\,\frac{\mathrm{m}}{\mathrm{s}}=-0.5\,\frac{\mathrm{m}}{\mathrm{s}}</math></center> | ||
| + | |||
| + | y para la masa 2 | ||
| + | |||
| + | <center><math>v_{2f}=\frac{2m_1}{m_1+m_2}v_{2i}=\frac{2\cdot 100}{100+300}\cdot 1.0\,\frac{\mathrm{m}}{\mathrm{s}}=+0.5\,\frac{\mathrm{m}}{\mathrm{s}}</math></center> | ||
| + | |||
| + | Vemos que las dos masas se alejan con velocidades iguales y opuestas. | ||
| + | |||
| + | ==Movimiento de la masa 2== | ||
| + | Una vez que empieza a deslizarse por el plano, la masa 2 experimenta una fuerza de rozamiento proporcional a la normal, que en este caso iguala al peso, | ||
| + | |||
| + | <center><math>|\vec{F}_r| = \mu |\vec{F}_n| = \mu m_2g</math></center> | ||
| + | |||
| + | Esta fuerza es horizontal y opuesta al movimiento | ||
| + | |||
| + | <center><math>\vec{F}_r = -\mu m_2g\vec{\imath}</math></center> | ||
| + | |||
| + | Por ser constante produce un movimiento uniformemente acelerado, con aceleración | ||
| + | |||
| + | <center><math>a_2 = \frac{F_r}{m}=-\mu g</math></center> | ||
| + | |||
| + | Integrando dos veces obtenemos la velocidad y la posición en cada instante | ||
| + | |||
| + | <center><math>v = v_{2f} - \mu g t\qquad\qquad x = v_{2f}t-\frac{1}{2}\mu g t^2</math></center> | ||
| + | |||
| + | El tiempo <math>T</math> hasta que la masa se para lo da el que la velocidad se anule | ||
| + | |||
| + | <center><math>0 = v_{2f}-\mu g T\qquad\Rightarrow\qquad T = \frac{v_{2f}}{\mu g}=\frac{0.5}{0.2\times 9.8}\,\mathrm{s}=0.255\,\mathrm{s}</math></center> | ||
| + | |||
| + | y la distancia recorrida hasta que se para es | ||
| + | |||
| + | <center><math>X = v_{2f}T-\frac{1}{2}\mu g T^2 = \frac{v_{2f}^2}{2\mu g}= \frac{v_{2f}T}{2}=0.0638\,\mathrm{m}=6.38\,\mathrm{cm}</math></center> | ||
| + | |||
| + | ==Contracción del muelle== | ||
| + | Tras la colisión, la masa 1 retrocede y vuelve a comprimir el muelle. La distancia que se comprime, <math>A'</math> la hallamos aplicando de nuevo la ley de conservación de la energía mecánica | ||
| + | |||
| + | <center><math>\frac{1}{2}mv_{1f}^2 = \frac{1}{2}kA'^2 \qquad\Rightarrow\qquad A' = \sqrt{\frac{m}{k}}v_{1f}=0.05\,\mathrm{m}=5\,\mathrm{cm}</math></center> | ||
| + | |||
| + | La amplitud en un movimiento armónico simple es proporcional a la rapidez en el punto de equilibrio, así que si ésta es la mitad que antes, la amplitud resultante también es la mitad de la primera. | ||
[[Categoría:Problemas de dinámica de los sistemas de partículas (GIE)]] | [[Categoría:Problemas de dinámica de los sistemas de partículas (GIE)]] | ||
| + | [[Categoría:Problemas de dinámica de la partícula (GIE)]] | ||
última version al 20:19 6 sep 2012
Contenido |
1 Enunciado
Sobre una mesa horizontal se encuentra un bloque de masa 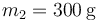 . Para lanzarlo por el plano se emplea un resorte de constante
. Para lanzarlo por el plano se emplea un resorte de constante  en cuyo extremo se encuentra una masa
en cuyo extremo se encuentra una masa 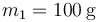 . En la posición de equilibrio, las dos masas se tocan. El resorte no tiene rozamiento alguno. La masa m2 tiene un coeficiente de rozamiento (estático y dinámico) μ = 0.2 con la mesa.
. En la posición de equilibrio, las dos masas se tocan. El resorte no tiene rozamiento alguno. La masa m2 tiene un coeficiente de rozamiento (estático y dinámico) μ = 0.2 con la mesa.
Se comprime el resorte una distancia 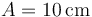 y a continuación se libera, para que golpee a la masa m2 y esta salga disparada.
y a continuación se libera, para que golpee a la masa m2 y esta salga disparada.
- Halle la velocidad que lleva la masa m1 en el momento del impacto.
- Suponiendo que el choque es elástico, calcule las velocidades que tienen las masas justo tras la colisión.
- Calcule la distancia recorrida por m2 hasta que se para y el tiempo que tarda en hacerlo.
- Halle cuánto se vuelve a contraer el muelle tras la colisión.

2 Velocidad del resorte
La masa unida al resorte no experimenta fuerzas de rozamiento y está sometida exclusivamente a fuerzas conservativas y por tanto se conserva la energía mecánica.
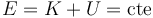
La energía potencial es la suma de la gravitatoria (que es constante, por ser la superficie horizontal) y la elástica. Podemos ignorar la gravitatoria, pues siempre va a tener el mismo valor. Esto nos deja con la ley de conservación
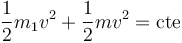
Para hallar la velocidad de impacto, igualamos la energía mecánica en el momento de máxima compresión, con la que tiene la masa 1 en el momento del golpe. En el primer caso, la masa está instantáneamente en reposo y su energía cinética es nula, y en el segundo se halla en la posición de equilibrio, por lo que se anula su energía potencial. Esto nos da
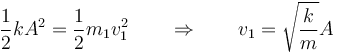
Sustituyendo los valores numéricos
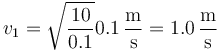
3 Velocidades tras la colisión
Una vez que se produce la colisión tanto la masa unida al muelle, como la que se encuentra sobre el plano, tienen nuevas velocidades. Para hallarlas aplicamos la ley de conservación de la cantidad de movimiento
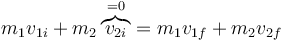
y que la colisión es perfectamente elástica, con lo que se conserva la energía cinética del sistema, o equivalentemente, el coeficiente de restitución es la unidad
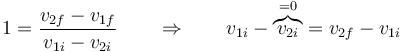
Resolviendo el sistema de dos ecuaciones con dos incógnitas queda
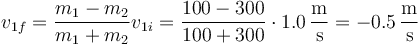
y para la masa 2
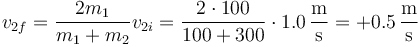
Vemos que las dos masas se alejan con velocidades iguales y opuestas.
4 Movimiento de la masa 2
Una vez que empieza a deslizarse por el plano, la masa 2 experimenta una fuerza de rozamiento proporcional a la normal, que en este caso iguala al peso,
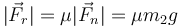
Esta fuerza es horizontal y opuesta al movimiento
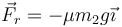
Por ser constante produce un movimiento uniformemente acelerado, con aceleración
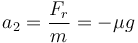
Integrando dos veces obtenemos la velocidad y la posición en cada instante

El tiempo T hasta que la masa se para lo da el que la velocidad se anule
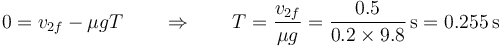
y la distancia recorrida hasta que se para es

5 Contracción del muelle
Tras la colisión, la masa 1 retrocede y vuelve a comprimir el muelle. La distancia que se comprime, A' la hallamos aplicando de nuevo la ley de conservación de la energía mecánica
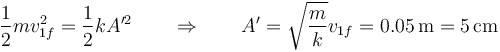
La amplitud en un movimiento armónico simple es proporcional a la rapidez en el punto de equilibrio, así que si ésta es la mitad que antes, la amplitud resultante también es la mitad de la primera.





