Coeficientes de inducción de dos bobinas (F2GIA)
De Laplace
(→Solución) |
(→Enunciado) |
||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
Se tienen dos bobinas o solenoides, ambas de igual longitud <math>h</math>, pero de distinta sección: la bobina “1” tiene forma de cilindro recto, estando formada por <math>N_1</math> espiras circulares de radio <math>a</math>. Por su parte, la bobina “2” tiene forma de prisma recto de sección cuadrada y la constituyen <math>N_2</math> espiras cuadradas iguales, cuya diagonal mide <math>2a</math>. En ambas bobinas los hilos conductores están enrollados en el mismo sentido, y de manera que las espiras se distribuyen de forma compacta en planos perpendiculares a su correspondiente eje. Asumiendo que se verifica la condición de bobinas largas (<math>h\gg 2a</math>), ¿cuáles son los coeficientes de autoinducción y de inducción mutua del sistema cuando la bobina “2” se coloca por completo en el interior de la “1”? | Se tienen dos bobinas o solenoides, ambas de igual longitud <math>h</math>, pero de distinta sección: la bobina “1” tiene forma de cilindro recto, estando formada por <math>N_1</math> espiras circulares de radio <math>a</math>. Por su parte, la bobina “2” tiene forma de prisma recto de sección cuadrada y la constituyen <math>N_2</math> espiras cuadradas iguales, cuya diagonal mide <math>2a</math>. En ambas bobinas los hilos conductores están enrollados en el mismo sentido, y de manera que las espiras se distribuyen de forma compacta en planos perpendiculares a su correspondiente eje. Asumiendo que se verifica la condición de bobinas largas (<math>h\gg 2a</math>), ¿cuáles son los coeficientes de autoinducción y de inducción mutua del sistema cuando la bobina “2” se coloca por completo en el interior de la “1”? | ||
| - | |||
| - | |||
[[Categoría:Problemas de examen F2 GIA]] | [[Categoría:Problemas de examen F2 GIA]] | ||
Revisión de 11:07 15 jul 2012
1 Enunciado
Se tienen dos bobinas o solenoides, ambas de igual longitud h, pero de distinta sección: la bobina “1” tiene forma de cilindro recto, estando formada por N1 espiras circulares de radio a. Por su parte, la bobina “2” tiene forma de prisma recto de sección cuadrada y la constituyen N2 espiras cuadradas iguales, cuya diagonal mide 2a. En ambas bobinas los hilos conductores están enrollados en el mismo sentido, y de manera que las espiras se distribuyen de forma compacta en planos perpendiculares a su correspondiente eje. Asumiendo que se verifica la condición de bobinas largas (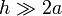
), ¿cuáles son los coeficientes de autoinducción y de inducción mutua del sistema cuando la bobina “2” se coloca por completo en el interior de la “1”?
2 Solución
y 
, que cuando son recorridos por corrientes de intensidad I1 eI2, respectivamente, generarán campos magnéticos tales que los flujos del campo magnético total a través aquéllas verificarán las relaciones,
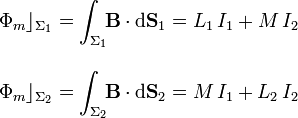
donde L1 y L2 son los coeficientes de autoinducción de las bobinas, y M el de inducción mutua. Y puesto que estos coeficientes están directamente relacionados con los flujos magnéticos a través de superificies Σ1 y Σ2 delimitadas por los circuitos 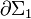y 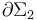, van de depender tanto de su forma y geometría como de su disposición relativa.
