Cálculo de flujo
De Laplace
(Diferencias entre revisiones)
(Nueva página: ==Enunciado== Para el campo vectorial <center><math>\mathbf{A} = (x-y)\mathbf{u}_{x}+(x+y)\mathbf{u}_{y}+z\mathbf{u}_{z}\,</math></center> calcule su flujo a través de las siguient...) |
(→Superficie cúbica) |
||
| Línea 14: | Línea 14: | ||
==Solución== | ==Solución== | ||
===Superficie cúbica=== | ===Superficie cúbica=== | ||
| + | [[Imagen:supcubica.gif|right]]Para el flujo a través de un cubo, descomponemos la integral en seis partes, una por cada cara. | ||
| + | |||
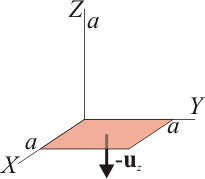
| + | ====Cara inferior==== | ||
| + | [[Imagen:cubo-cara1.gif|left]]Para la cara inferior (<math>z=0</math>), el campo en estos puntos vale | ||
| + | |||
| + | <center><math>\mathbf{A}(z=0) = (x-y)\mathbf{u}_{x}+(x+y)\mathbf{u}_{y}</math></center> | ||
| + | |||
| + | y el vector diferencial de superficie dirigido al exterior | ||
| + | |||
| + | <center><math>\mathrm{d}\mathbf{S} = -\mathrm{d}{x}\,\mathrm{d}{y}\,\mathbf{u}_{z}</math></center> | ||
| + | |||
| + | Al ser ortogonales estos dos vectores el flujo elemental vale | ||
| + | |||
| + | <center><math>\Phi_1 = \int \mathbf{A}{\cdot}\mathrm{d}{\mathbf{S}} = \int_0^a \int_0^a 0\,\mathrm{d}{x}\mathrm{d}{y} = 0</math></center> | ||
| + | |||
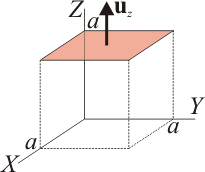
| + | ====Cara superior==== | ||
| + | [[Imagen:cubo-cara2.gif|right]]En la cara superior (<math>z=a</math>) el vector <math>\mathbf{A}</math> vale | ||
| + | |||
| + | <center><math>\mathbf{A} = (x-y)\mathbf{u}_{x}+(x+y)\mathbf{u}_{y}+a\mathbf{u}_{z}</math></center> | ||
| + | |||
| + | y el diferencial de superficie | ||
| + | |||
| + | <center><math>\mathrm{d}{\mathbf{S}}= \mathrm{d}{x}\,\mathrm{d}{y}\,\mathbf{u}_{z}</math></center> | ||
| + | |||
| + | y resulta el flujo elemental | ||
| + | |||
| + | <center><math>\Phi_2 = \int_0^a\int_0^a a\,\mathrm{d}{x}\,\mathrm{d}{y}= a^3</math></center> | ||
| + | |||
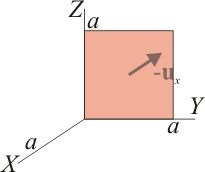
| + | ====Cara del fondo==== | ||
| + | [[Imagen:cubo-cara3.gif|left]]Para la cara del fondo (<math>x=0</math>) | ||
| + | |||
| + | <math>\mathbf{A}(x=0) = -y\mathbf{u}_{x}+y\mathbf{u}_{y}+z\mathbf{u}_{z}</math>{{qquad}}{{qquad}} | ||
| + | <math>\mathrm{d}{\mathbf{S}} = -\mathrm{d}{y}\,\mathrm{d}{z}\,\mathbf{u}_{x}</math> | ||
| + | |||
| + | con lo que el flujo elemental es | ||
| + | |||
| + | <center><math>\Phi_3 = \int_0^a\int_0^a y \,\mathrm{d}{y}\,\mathrm{d}{z}= \frac{a^3}{2}</math></center> | ||
| + | |||
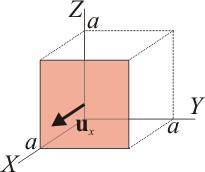
| + | ====Cara frontal==== | ||
| + | [[Imagen:cubo-cara4.gif|right]]Para la cara frontal (<math>x=a</math>) | ||
| + | |||
| + | <center><math>\mathbf{A} = (a-y)\mathbf{u}_{x}+(a+y)\mathbf{u}_{y}+z\mathbf{u}_{z}</math>{{qquad}}{{qquad}} | ||
| + | <math>\mathrm{d}{\mathbf{S}} = \mathrm{d}{y}\,\mathrm{d}{z}\,\mathbf{u}_{x}</math></center> | ||
| + | |||
| + | |||
| + | <center><math>\Phi_4 = \int_0^a\int_0^a (a-y)\,\mathrm{d}{y}\,\mathrm{d}{z} = \frac{a^3}{2} | ||
| + | </math></center> | ||
| + | |||
| + | ====Cara izquierda==== | ||
| + | Para la cara izquierda (<math>y=0</math>) | ||
| + | |||
| + | <center><math>\mathbf{A} = x\mathbf{u}_{x}+x\mathbf{u}_{y}+z\mathbf{u}_{z}</math>{{qquad}}{{qquad}} | ||
| + | <math>\mathrm{d}{\mathbf{S}} = -\mathrm{d}{x}\,\mathrm{d}{z}\,\mathbf{u}_{y}</math></center> | ||
| + | |||
| + | |||
| + | <center><math>\Phi_5 = -\int_0^a\int_0^a x\,\mathrm{d}{x}\,\mathrm{d}{z} = -\frac{a^3}{2}</math></center> | ||
| + | |||
| + | <center>[[Imagen:cubo-cara5|Cara izquierda]]{{qquad}}[[Imagen:cubo-cara5|Cara izquierda|Cara derecha]]</center> | ||
| + | |||
| + | ====Cara derecha==== | ||
| + | Para la cara derecha (<math>y=a</math>) | ||
| + | |||
| + | <center><math>\mathbf{A} = (x-a)\mathbf{u}_{x}+(x+a)\mathbf{u}_{y}+z\mathbf{u}_{z}</math>{{qquad}}{{qquad}} | ||
| + | <math>\mathrm{d}{\mathbf{S}} = \mathrm{d}{x}\,\mathrm{d}{z}\,\mathbf{u}_{y}</math></center> | ||
| + | |||
| + | |||
| + | <math>\Phi_6 = \int_0^a\int_0^a (x+a)\,\mathrm{d}{x}\,\mathrm{d}{z} = \frac{3a^3}{2}</math> | ||
| + | |||
| + | Sumando las seis contribuciones tenemos el flujo total | ||
| + | |||
| + | <math>\Phi = 0+a^3 + \frac{a^3}{2}+\frac{a^3}{2}-\frac{a^3}{2}+\frac{3a^3}{2} | ||
| + | = 3a^3</math> | ||
| + | |||
| + | Este mismo cálculo, por aplicación del teorema de Gauss queda | ||
| + | |||
| + | <center><math>\nabla{\cdot}\mathbf{A} = 1+1+1 = 3</math></center> | ||
| + | |||
| + | |||
| + | <center><math>\Phi = \int_0^a\int_0^a\int_0^a 3 \mathrm{d}{x}\,\mathrm{d}{y}\,\mathrm{d}{z} = 3a^3 = 3\tau</math></center> | ||
| + | |||
| + | Dado que la divergencia es una constante, su integral de volumen es simplemente el producto de esta constante (3) por el volumen del | ||
| + | dominio. | ||
| + | |||
===Superficie cilíndrica=== | ===Superficie cilíndrica=== | ||
===Superficie esférica=== | ===Superficie esférica=== | ||
[[Categoría:Problemas de fundamentos matemáticos]] | [[Categoría:Problemas de fundamentos matemáticos]] | ||
Revisión de 15:53 1 oct 2008
Contenido |
1 Enunciado
Para el campo vectorial
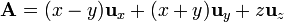
calcule su flujo a través de las siguientes superficies cerradas:
- Un cubo de arista a, con un vértice en el origen y aristas
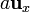 ,
, 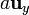 y
y 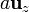 .
.
- Un cilindro circular de altura h y radio R, con el eje Z como eje y sus bases situadas en z = 0 y z = h.
- Una esfera de radio R en torno al origen de coordenadas.
En cada caso, halle el flujo por integración directa y por aplicación del teorema de Gauss.
2 Solución
2.1 Superficie cúbica
Para el flujo a través de un cubo, descomponemos la integral en seis partes, una por cada cara.2.1.1 Cara inferior
Para la cara inferior (z = 0), el campo en estos puntos vale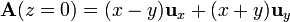
y el vector diferencial de superficie dirigido al exterior
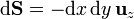
Al ser ortogonales estos dos vectores el flujo elemental vale

2.1.2 Cara superior
En la cara superior (z = a) el vector vale
vale

y el diferencial de superficie
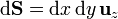
y resulta el flujo elemental

2.1.3 Cara del fondo
Para la cara del fondo (x = 0)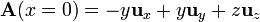
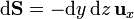
con lo que el flujo elemental es
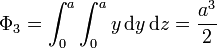
2.1.4 Cara frontal
Para la cara frontal (x = a)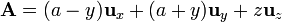
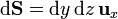
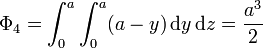
2.1.5 Cara izquierda
Para la cara izquierda (y = 0)

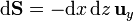

2.1.6 Cara derecha
Para la cara derecha (y = a)

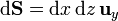
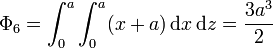
Sumando las seis contribuciones tenemos el flujo total
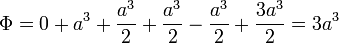
Este mismo cálculo, por aplicación del teorema de Gauss queda
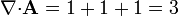
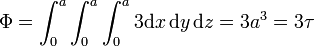
Dado que la divergencia es una constante, su integral de volumen es simplemente el producto de esta constante (3) por el volumen del dominio.