Construcción de una bobina
De Laplace
(→Tiempo de decaimiento) |
|||
| (Una edición intermedia no se muestra.) | |||
| Línea 83: | Línea 83: | ||
Alternativamente, si lo que hemos hallado es la energía, esta fórmula permite calcular el coeficiente de autoinducción. | Alternativamente, si lo que hemos hallado es la energía, esta fórmula permite calcular el coeficiente de autoinducción. | ||
==Tiempo de decaimiento== | ==Tiempo de decaimiento== | ||
| + | Cuando se cortocircuita la bobina, la ecuación que describe la corriente es | ||
| + | |||
| + | <center><math>L\frac{\mathrm{d}I}{\mathrm{d}t}+IR=0</math></center> | ||
| + | |||
| + | cuya solución es un decaimiento exponencial | ||
| + | |||
| + | <center><math>I =I_0\mathrm{e}^{-t/\tau}</math></center> | ||
| + | |||
| + | siendo el tiempo de descarga | ||
| + | |||
| + | <center><math>\tau = \frac{L}{R}=\frac{0.334\,\mathrm{mH}}{2.10\,\Omega}=0.159\,\mathrm{ms}</math></center> | ||
| + | |||
| + | Este es el orden de magnitud del tiempo de decaimiento, aunque es más correcto considerar como tiempò unas 4 o 5 veces este, de forma que la corriente ya se ha reducido a menos de un 1% de la inicial, En ese caso | ||
| + | |||
| + | <center><math>T = 5\tau \sim 0.8\,\mathrm{ms}</math></center> | ||
| + | |||
| + | es decir, en un tiempo del orden de un milisegundo desparece la corriente en la bobina. | ||
[[Categoría:Problemas de campo magnético de corrientes estacionarias]] | [[Categoría:Problemas de campo magnético de corrientes estacionarias]] | ||
[[Categoría:Problemas de inducción electromagnética]] | [[Categoría:Problemas de inducción electromagnética]] | ||
última version al 23:04 19 jun 2012
Contenido |
1 Enunciado
Se dispone de una bobina de 26 mm de diámetro y 300 vueltas, construida con un hilo de cobre de sección circular de 0.5 mm de diámetro que se enrolla dejando un espacio de 0.1 mm entre vuelta y vuelta.
- Calcule la resistencia de la bobina, el voltaje que hay que aplicar entre los extremos para que circule por ella una corriente de 0.5 A y el calor generado por segundo en ella por efecto Joule.
- Halle el valor aproximado del campo magnético que se produce en el interior de la bobina para esta corriente, así como el de la energía magnética almacenada en ella.
- Calcule el coeficiente de autoinducción de la bobina.
- Suponga que se cortocircuita la fuente, ¿cuánto tiempo tarda aproximadamente en desaparecer la corriente que circula por la bobina?
2 Resistencia, voltaje y calor
2.1 Resistencia
La bobina es un hilo de cobre enrollado, por lo que se aplica la fórmula para un conductor filiforme

siendo l la longitud del hilo, que es aproximadamente igual a la longitud de las N espiras circulares (habría una pequeñísima corrección debido a que realmente se trata de una hélice)

La sección es la correspondiente a una circunferencia de diámetro 0.5mm

lo que nos da la resistencia

2.2 Voltaje
Una vez que tenemos la resistencia, el cálculo del voltaje es inmediato, sin más que aplicar la ley de Ohm

2.3 Potencia disipada
La potencia disipada la obtenemos por aplicación de la ley de Joule

3 Campo y energía magnética
El campo magnético creado en el interior de una bobina larga vale, aproximadamente,

siendo
-

-

-

- h es la longitud de la bobina, igual a la suma de los diámetros y los espacios entre vuelta y vuelta

lo que da el valor del campo

Una vez que tenemos el valor del campo, podemos hallar la energía a partir de la integral de volumen
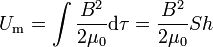
siendo S la sección transversal de la bobina (no del hilo)
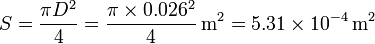
lo que nos da la energía
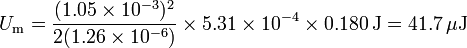
La energía también puede hallarse a partir del coeficiente de autoinducción que se calcula en el apartado siguiente.
4 Coeficiente de autoinducción
El coeficiente de autoinducción de una bobina larga puede calcularse de manera aproximada mediante la fórmula

que para nuestro caso da

Este coeficiente de autoinducción permite hallar la energía magnética almacenada según la fórmula
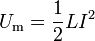
Alternativamente, si lo que hemos hallado es la energía, esta fórmula permite calcular el coeficiente de autoinducción.
5 Tiempo de decaimiento
Cuando se cortocircuita la bobina, la ecuación que describe la corriente es

cuya solución es un decaimiento exponencial
siendo el tiempo de descarga

Este es el orden de magnitud del tiempo de decaimiento, aunque es más correcto considerar como tiempò unas 4 o 5 veces este, de forma que la corriente ya se ha reducido a menos de un 1% de la inicial, En ese caso

es decir, en un tiempo del orden de un milisegundo desparece la corriente en la bobina.





