Circuito variable en plano inclinado (F2GIA)
De Laplace
(→Flujo del campo magnético a través del circuito) |
(→Intensidad de corriente y velocidad límite) |
||
| Línea 15: | Línea 15: | ||
<center>[[Archivo:bol_6_ej_4_2.gif]]</center> | <center>[[Archivo:bol_6_ej_4_2.gif]]</center> | ||
| - | Adoptamos un sistema de referencia cartesiano cuyo eje <math>X</math> es paralelo a las guías, y con el eje <math>Y</math> perpendicular al plano inclinado que las soporta. La varilla móvil se mantendrá siempre paralela al eje <math>X</math>, y su desplazamiento estará descrito por una vector velocidad <math>\ | + | Adoptamos un sistema de referencia cartesiano cuyo eje <math>X</math> es paralelo a las guías, y con el eje <math>Y</math> perpendicular al plano inclinado que las soporta. La varilla móvil se mantendrá siempre paralela al eje <math>X</math>, y su desplazamiento estará descrito por una vector velocidad <math>\mathbf{v}(t)=v(t)\!\ \mathbf{i}</math>. |
====Flujo del campo magnético a través del circuito==== | ====Flujo del campo magnético a través del circuito==== | ||
En primer lugar, procederemos a discutir acerca del campo magnético existente en el el entorno del circuito: por un lado, está el campo uniforme aplicado en la dirección de la vertical gravitatoria, y cuya descripción analítica en el sistema de referencia adoptado será: | En primer lugar, procederemos a discutir acerca del campo magnético existente en el el entorno del circuito: por un lado, está el campo uniforme aplicado en la dirección de la vertical gravitatoria, y cuya descripción analítica en el sistema de referencia adoptado será: | ||
| - | <center><math>\ | + | <center><math>\mathbf{B}_0=B_0\!\ \left(-\,\mathrm{sen}\,\alpha\!\ \mathbf{i}+\cos\alpha\!\ \mathbf{j}\right)\mathrm{,}\quad\,\mathrm{con}\,\;\;B_0=|\mathbf{B}_0|=0.5\,\mathrm{T}\,</math></center> |
Pero si el movimiento de la varilla tiene como consecuencia la aparición de una fuerza electromotriz y una corriente <math>I</math> inducidas, esta última será fuentes de un campo magnético, que denominaremos <math>\vec{B}_\mathrm{ind}</math>, y que también contribuirá al flujo magnético a través de la superficie delimitada por el circuito/espira <math>\partial S</math>. Nótese que este flujo del ''campo inducido'' va a ser proporcional a la intensidad de corriente <math>I</math> que lo genera, siendo la constante de proporcionalidad la '''autoinducción ''' <math>L</math> de la espira que, por otra parte, será variable al cambiar la forma de la ésta: | Pero si el movimiento de la varilla tiene como consecuencia la aparición de una fuerza electromotriz y una corriente <math>I</math> inducidas, esta última será fuentes de un campo magnético, que denominaremos <math>\vec{B}_\mathrm{ind}</math>, y que también contribuirá al flujo magnético a través de la superficie delimitada por el circuito/espira <math>\partial S</math>. Nótese que este flujo del ''campo inducido'' va a ser proporcional a la intensidad de corriente <math>I</math> que lo genera, siendo la constante de proporcionalidad la '''autoinducción ''' <math>L</math> de la espira que, por otra parte, será variable al cambiar la forma de la ésta: | ||
| - | <center><math>\Phi_m\big\rfloor_S(t)=\ | + | <center><math>\Phi_m\big\rfloor_S(t)=\int_{S(t)}\!\mathbf{B}\cdot\mathrm{d} ºmathbf{S}</math></center> |
====Expresión de la intensidad de corriente==== | ====Expresión de la intensidad de corriente==== | ||
Revisión de 11:34 2 jun 2012
Contenido |
1 Enunciado
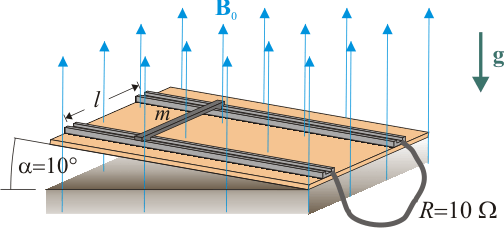
Una varilla conductora de masa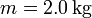 se deja caer deslizando sin rozamiento por dos guías metálicas paralelas separadas una distancia
se deja caer deslizando sin rozamiento por dos guías metálicas paralelas separadas una distancia 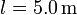 contenidas en un plano inclinado que forma un ángulo α = 10o con la horizontal. La dirección de la varilla es, en todo instante, perpendicular a las guías, las cuáles tienen conectados sus extremos mediante un cable de resistencia eléctrica
contenidas en un plano inclinado que forma un ángulo α = 10o con la horizontal. La dirección de la varilla es, en todo instante, perpendicular a las guías, las cuáles tienen conectados sus extremos mediante un cable de resistencia eléctrica 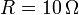 , que cierra el circuito. Las resistencias eléctricas de la varilla y las guías son despreciables. El sistema descrito se halla inmerso en un campo magnético uniforme y constante,
, que cierra el circuito. Las resistencias eléctricas de la varilla y las guías son despreciables. El sistema descrito se halla inmerso en un campo magnético uniforme y constante,  , de
, de 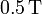 de intensidad, aplicado en dirección vertical y sentido contrario a la gravedad. Calcule:
de intensidad, aplicado en dirección vertical y sentido contrario a la gravedad. Calcule:
- Corriente inducida en el circuito y velocidad límite que alcanzará la varilla.
- Potencia disipada por efecto Joule en la resistencia. Compare esta potencia con el trabajo que por unidad de tiempo realiza la fuerza peso sobre la varilla.
2 Solución
Las dos guías paralelas conectadas por el cable y en contacto con la varilla móvil, constituyen un circuito cerrado 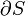 por el que puede circular una corriente eléctrica, al tratarse de materiales conductores. Al poder desplazarse la varilla sobre las guías, se trata de un circuito variable en el que las resistencias eléctricas de estos elementos son despreciables frente a la
por el que puede circular una corriente eléctrica, al tratarse de materiales conductores. Al poder desplazarse la varilla sobre las guías, se trata de un circuito variable en el que las resistencias eléctricas de estos elementos son despreciables frente a la 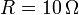 del cable.
del cable.
2.1 Intensidad de corriente y velocidad límite
Consideremos la superficie plana S delimitada por el circuito 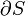 . La acción de la gravedad sobre la varilla pesada provoca el deslizamiento (sin rozamiento apreciable) de ésta sobre las guías inclinadas un ángulo α respecto de la horizontal y, por tanto, la variación del área de dicha superficie, S = S(t). Esto se traducirá también en la variación del flujo a través de aquélla del campo magnético existente y, en virtud de la ley de inducción electromagnética, producirá una fuerza electromotriz inducida y una intensidad de corriente I en el circuito
. La acción de la gravedad sobre la varilla pesada provoca el deslizamiento (sin rozamiento apreciable) de ésta sobre las guías inclinadas un ángulo α respecto de la horizontal y, por tanto, la variación del área de dicha superficie, S = S(t). Esto se traducirá también en la variación del flujo a través de aquélla del campo magnético existente y, en virtud de la ley de inducción electromagnética, producirá una fuerza electromotriz inducida y una intensidad de corriente I en el circuito 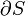 .
.
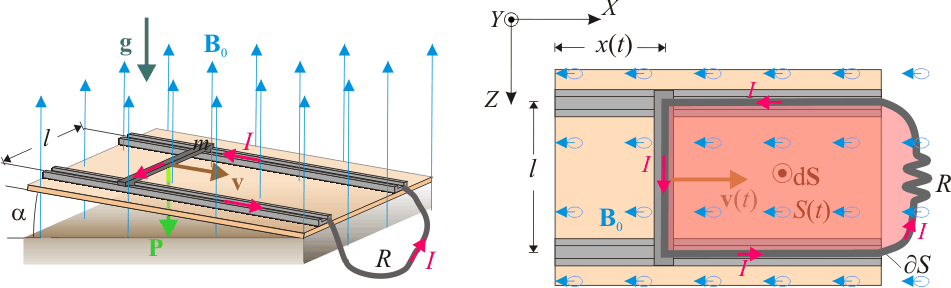
Adoptamos un sistema de referencia cartesiano cuyo eje X es paralelo a las guías, y con el eje Y perpendicular al plano inclinado que las soporta. La varilla móvil se mantendrá siempre paralela al eje X, y su desplazamiento estará descrito por una vector velocidad 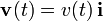 .
.
2.1.1 Flujo del campo magnético a través del circuito
En primer lugar, procederemos a discutir acerca del campo magnético existente en el el entorno del circuito: por un lado, está el campo uniforme aplicado en la dirección de la vertical gravitatoria, y cuya descripción analítica en el sistema de referencia adoptado será:
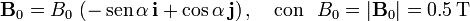
Pero si el movimiento de la varilla tiene como consecuencia la aparición de una fuerza electromotriz y una corriente I inducidas, esta última será fuentes de un campo magnético, que denominaremos  , y que también contribuirá al flujo magnético a través de la superficie delimitada por el circuito/espira
, y que también contribuirá al flujo magnético a través de la superficie delimitada por el circuito/espira 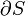 . Nótese que este flujo del campo inducido va a ser proporcional a la intensidad de corriente I que lo genera, siendo la constante de proporcionalidad la autoinducción L de la espira que, por otra parte, será variable al cambiar la forma de la ésta:
. Nótese que este flujo del campo inducido va a ser proporcional a la intensidad de corriente I que lo genera, siendo la constante de proporcionalidad la autoinducción L de la espira que, por otra parte, será variable al cambiar la forma de la ésta: