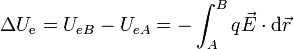Potencial y energía electrostática (GIE)
De Laplace
| Línea 1: | Línea 1: | ||
| - | == | + | ==Trabajo y energía potencial== |
===Trabajo para mover una carga eléctrica=== | ===Trabajo para mover una carga eléctrica=== | ||
Supongamos que tenemos una carga positiva “1” en una posición fija del espacio, y deseamos acercar otra carga positiva “2” desde un punto A a un punto B más próximo a la primera. Para hacerlo debemos vencer la repulsión eléctrica ejercida por la primera, aplicando una fuerza externa. | Supongamos que tenemos una carga positiva “1” en una posición fija del espacio, y deseamos acercar otra carga positiva “2” desde un punto A a un punto B más próximo a la primera. Para hacerlo debemos vencer la repulsión eléctrica ejercida por la primera, aplicando una fuerza externa. | ||
| Línea 17: | Línea 17: | ||
Este razonamiento es generalizable al movimiento de una carga en un campo eléctrico cualquiera (no necesariamente el de una sola carga, sino el de una distribución). Al mover la carga debemos realizar un trabajo, que queda guardado como energía potencial electrostática. | Este razonamiento es generalizable al movimiento de una carga en un campo eléctrico cualquiera (no necesariamente el de una sola carga, sino el de una distribución). Al mover la carga debemos realizar un trabajo, que queda guardado como energía potencial electrostática. | ||
| + | ===Energía potencial electrostática=== | ||
| + | Para hallar una expresión para la energía potencial suponemos que movemos una carga el seno de un campo eléctrico de manera cuasiestática. Para ello debemos ejercer una fuerza que supere a la eléctrica, pero solo ligeramente (pues la partícula no se llega a acelerar) | ||
| + | <center><math>\vec{F}_\mathrm{ext}+\vec{F}_e = \overbrace{m\vec{a}}^{=\vec{0}}\qquad\Rightarrow\qquad \vec{F}_\mathrm{ext}=-\vec{F}_e = -q\vec{E}</math></center> | ||
| + | |||
| + | por lo que el trabajo realizado es | ||
| + | |||
| + | <center><math>W_\mathrm{in} = -\int_A^B q\vec{E}\cdot\mathrm{d}\vec{r}</math></center> | ||
| + | |||
| + | En principio, esta integral depende del camino que se recorra. Sin embargo, para el caso del campo de una carga puntual es fácil demostrar (como veremos) que solo depende de la distancia inicial y final a la carga que crea el campo. Puesto que todo campo electrostático es suma de campos de cargas puntuales, se llega a que para cualquier campo electrostático, la integral es independiente del camino y equivale al incremento de una energía potencial | ||
| + | |||
| + | <center><math>\Delta U_\mathrm{e} = U_{eB}-U_{eA}=-\int_A^B q\vec{E}\cdot\mathrm{d}\vec{r}</math></center> | ||
==Potencial eléctrico== | ==Potencial eléctrico== | ||
==Energía electrostática de un sistema== | ==Energía electrostática de un sistema== | ||
[[Categoría:Electrostática en el vacío (GIE)]] | [[Categoría:Electrostática en el vacío (GIE)]] | ||
[[Categoría:Electricidad y magnetismo (GIE)]] | [[Categoría:Electricidad y magnetismo (GIE)]] | ||
Revisión de 12:01 27 may 2012
Contenido |
1 Trabajo y energía potencial
1.1 Trabajo para mover una carga eléctrica
Supongamos que tenemos una carga positiva “1” en una posición fija del espacio, y deseamos acercar otra carga positiva “2” desde un punto A a un punto B más próximo a la primera. Para hacerlo debemos vencer la repulsión eléctrica ejercida por la primera, aplicando una fuerza externa.
Por tanto, para acercar la carga debemos realizar un trabajo
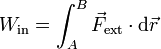
De acuerdo con el primer principio de la termodinámica, este trabajo realizado sobre el sistema, o bien se almacena como un aumento de la energía total, o bien sale en forma de calor (o una parte de cada cosa)
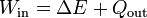
Si el proceso es cuasiestático, moviendo la carga 2 de forma extremadamente lenta, este trabajo se almacena en forma de energía potencial (que es parte de la energía total). Podemos verlo con el siguiente experimento mental: si una vez en la posición final B, sujetamos la carga 2 con una chincheta y esperamos un cierto tiempo, tras el cual la liberamos, la carga 2 sale disparada por la repulsión de la 1. Al hacerlo, gana energía cinética, ¿de dónde sale esta energía? No vale decir que se la da la carga 1 por su fuerza eléctrica, pues la energía se conserva y la carga 1 no pierde nada. Concluimos entonces, que la carga 2 ya tenía esa energía “guardada” en forma de energía potencial por el hecho de estar en presencia de la 1.
Usando la analogía mecánica, sería equivalente a comprimir un muelle (invisible), realizando para ello una fuerza en contra de la elástica. Se sujeta el muelle con un tope y pasado un tiempo, se retira éste. El muelle se estira empujando la masa, que se acelera. Podemos decir que la energía cinética que gana procede de la energía potencial elástica que tenía por estar el muelle comprimido.
Este razonamiento es generalizable al movimiento de una carga en un campo eléctrico cualquiera (no necesariamente el de una sola carga, sino el de una distribución). Al mover la carga debemos realizar un trabajo, que queda guardado como energía potencial electrostática.
1.2 Energía potencial electrostática
Para hallar una expresión para la energía potencial suponemos que movemos una carga el seno de un campo eléctrico de manera cuasiestática. Para ello debemos ejercer una fuerza que supere a la eléctrica, pero solo ligeramente (pues la partícula no se llega a acelerar)
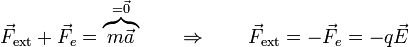
por lo que el trabajo realizado es
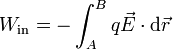
En principio, esta integral depende del camino que se recorra. Sin embargo, para el caso del campo de una carga puntual es fácil demostrar (como veremos) que solo depende de la distancia inicial y final a la carga que crea el campo. Puesto que todo campo electrostático es suma de campos de cargas puntuales, se llega a que para cualquier campo electrostático, la integral es independiente del camino y equivale al incremento de una energía potencial