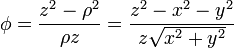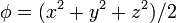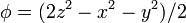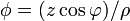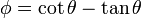Campos escalares en diferentes sistemas
De Laplace
(Diferencias entre revisiones)
(Nueva página: ==Enunciado== Exprese los siguientes campos escalares en coordenadas cartesianas, cilíndricas y esféricas # <math>\phi = (x^2+y^2+z^2)/2\,</math> # <math>\phi = (2z^2-x^2-y^2)/2\,<...) |
(→Tercer campo) |
||
| (Una edición intermedia no se muestra.) | |||
| Línea 8: | Línea 8: | ||
==Solución== | ==Solución== | ||
| + | No hay más que sustituir las relaciones entre los diferentes sistemas. | ||
| + | ===Primer campo=== | ||
| + | En el primer caso tenemos | ||
| + | |||
| + | <center><math>\phi = \frac{x^2+y^2+z^2}{2} = \frac{\rho^2+z^2}{2} = \frac{r^2}{2}</math></center> | ||
| + | |||
| + | ===Segundo campo=== | ||
| + | El segundo caso es similar al primero | ||
| + | |||
| + | <center><math>\phi = \frac{2z^2-x^2-y^2}{2} = \frac{2z^2-\rho^2}{2} = \frac{r^2(3\cos^2\theta-1)}{2}</math></center> | ||
| + | |||
| + | En otros problemas de fundamentos matemáticos se realizan cálculos adicionales con estos dos mismos campos. | ||
| + | |||
| + | ===Tercer campo=== | ||
| + | En el tercer caso, para pasar a cartesianas, conviene multiplicar y dividir por <math>\rho</math>. | ||
| + | |||
| + | <center><math>\phi = \frac{z\cos\varphi}{\rho} = \frac{z(\rho\cos\varphi)}{\rho^2} = \frac{zx}{x^2+y^2}</math></center> | ||
| + | |||
| + | y para pasar a esféricas basta con sustituir | ||
| + | |||
| + | <center><math>\phi = \frac{r\cos\theta\cos\varphi}{r\,\mathrm{sen}\,\theta} = \cot\theta\cos\varphi</math></center> | ||
| + | |||
| + | ===Cuarto campo=== | ||
| + | Para el último basta aplicar la relación | ||
| + | |||
| + | <center><math>\tan\theta = \frac{\rho}{z}</math></center> | ||
| + | |||
| + | con lo que queda | ||
| + | |||
| + | <center><math>\phi = \cot\theta-\tan\theta = \frac{z}{\rho}-\frac{\rho}{z} = \frac{z^2-\rho^2}{\rho z}</math></center> | ||
| + | |||
| + | y, en cartesianas, | ||
| + | |||
| + | <center><math>\phi = \frac{z^2-\rho^2}{\rho z} = \frac{z^2-x^2-y^2}{z\sqrt{x^2+y^2}}</math></center> | ||
| + | |||
[[Categoría:Problemas de fundamentos matemáticos]] | [[Categoría:Problemas de fundamentos matemáticos]] | ||
última version al 10:17 23 sep 2008
Contenido |
1 Enunciado
Exprese los siguientes campos escalares en coordenadas cartesianas, cilíndricas y esféricas
2 Solución
No hay más que sustituir las relaciones entre los diferentes sistemas.
2.1 Primer campo
En el primer caso tenemos
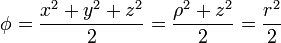
2.2 Segundo campo
El segundo caso es similar al primero
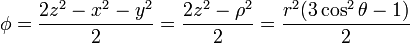
En otros problemas de fundamentos matemáticos se realizan cálculos adicionales con estos dos mismos campos.
2.3 Tercer campo
En el tercer caso, para pasar a cartesianas, conviene multiplicar y dividir por ρ.
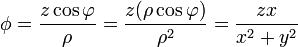
y para pasar a esféricas basta con sustituir
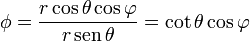
2.4 Cuarto campo
Para el último basta aplicar la relación

con lo que queda
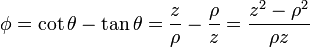
y, en cartesianas,