Conexiones de dos bombillas
De Laplace
| Línea 27: | Línea 27: | ||
La potencia disipada en las dos bombillas conjuntamente es | La potencia disipada en las dos bombillas conjuntamente es | ||
| - | <center><math> | + | <center><math>P_b = 2I^2 R_0 = \frac{2R_0\mathcal{E}^2}{(r+2R0)^2}</math></center> |
La potencia generada por la fuente vale | La potencia generada por la fuente vale | ||
| Línea 55: | Línea 55: | ||
<center><math>\mathcal{E}-2I_1r = I_1R_0\qquad\Rightarrow\qquad I_1 = \frac{\mathcal{E}}{2r+R_0}</math></center> | <center><math>\mathcal{E}-2I_1r = I_1R_0\qquad\Rightarrow\qquad I_1 = \frac{\mathcal{E}}{2r+R_0}</math></center> | ||
| + | y la potencia consumida en las dos bombillas es | ||
| + | <center><math>P_b=2I_1^2R_0 = \frac{2R_0\mathcal{E}^2}{(2r+R_0)^2}</math></center> | ||
| + | |||
| + | La potencia inyectada por la fuente en el sistema es, en este caso, | ||
| + | |||
| + | <center><math>P_g = I \mathcal{E}=2I_1 \mathcal{E}=\frac{2\mathcal{E}^2}{2r+R_0}</math></center> | ||
| + | |||
| + | y la consumida en la propia fuente | ||
| + | |||
| + | <center><math>P_r = I^2 r = 4I_1^2r = \frac{4r\mathcal{E}^2}{(2r+R_0)^2}</math></center> | ||
| + | |||
| + | cumpliéndose como antes que | ||
| + | |||
| + | <center><math>P_g = P_r + P_b\,</math></center> | ||
[[Categoría:Problemas de corriente eléctrica (GIE)]] | [[Categoría:Problemas de corriente eléctrica (GIE)]] | ||
Revisión de 19:54 22 may 2012
1 Enunciado
Se desea encender dos bombillas de resistencia R0, para lo cual se dispone de una batería de f.e.m.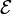 
y resistencia interna r.
- En un primer montaje se disponen las dos bombillas en serie.
- Calcule la intensidad de corriente que circula por cada una.
- Halle la potencia que consumen (que dará una medida de la luz que desprenden).
- Calcule la potencia desarrollada por el generador y el consumo de energía en el propio generador.
- A continuación se prueba a montarlas en paralelo.
- Calcule la intensidad de corriente que circula por cada una.
- Halle la potencia que consumen.
- Calcule la potencia desarrollada por el generador y el consumo de energía en el propio generador.
- ¿En cuál de los dos montajes el conjunto de las dos bombillas dará más luz?
- Supongamos que tenemos una batería de 10 V y 1 Ω de resistencia interna y dos bombillas en cuya etiqueta pone “10V 25W”, ¿cómo deberemos montarlas para que den el máximo de luz? ¿Cuánta potencia consumirán en ese caso?
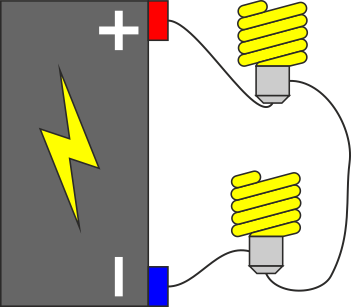
2 Bombillas en serie
Si las dos bombillas están en serie, el modelo del sistema es un circuito sencillo formado por cuatro elementos en serie:
- Una fuente ideal de f.e.m
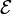
- La resistencia interna de la fuente, r
- Las dos resistencias de las dos bombillas.
En este circuito la corriente que circula por él es igual a la f.e.m. dividida por la suma de todas las resistencias
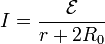
La potencia disipada en las dos bombillas conjuntamente es
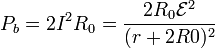
La potencia generada por la fuente vale
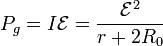
y la consumida en la propia fuente es la diferencia entre las dos anteriores
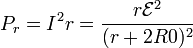
3 Bombillas en paralelo
Si las dos bombillas están en paralelo, la diferencia de potencial entre sus extremos es la misma para los dos e igual a la tensión a la salida de la fuente
siendo I1 la corriente que circula por una bombilla (que al ser las dos iguales, será idéntica a la que pasa por la otra).
La tensión a la salida de la fuente no es igual a la f.e.m., por no ser la fuente ideal, sino que hay una caída de tensión en la resistencia interna
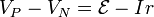
siendo
Nos queda entonces que la corriente que va por cada bombilla es
y la potencia consumida en las dos bombillas es
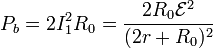
La potencia inyectada por la fuente en el sistema es, en este caso,
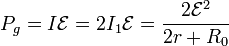
y la consumida en la propia fuente
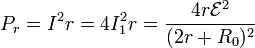
cumpliéndose como antes que
