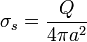Esfera conductora en equilibrio electrostático
De Laplace
(Página creada con '==Enunciado== Se tiene una esfera metálica maciza de radio <math>a</math> y no hay más conductores ni cargas en el sistema. Si la esfera almacena una carga total <math>Q</math…') |
|||
| Línea 11: | Línea 11: | ||
Suponga ahora que lo que se conoce inicialmente su voltaje <math>V_0</math>, pero no su carga. Halle en ese caso la carga que almacena, así como el resto de las cantidades obtenidas anteriormente. Particularice los resultados anteriores para un voltaje <math>V_0 = 12\,\mathrm{V}</math>. | Suponga ahora que lo que se conoce inicialmente su voltaje <math>V_0</math>, pero no su carga. Halle en ese caso la carga que almacena, así como el resto de las cantidades obtenidas anteriormente. Particularice los resultados anteriores para un voltaje <math>V_0 = 12\,\mathrm{V}</math>. | ||
==Potencial y campo eléctrico== | ==Potencial y campo eléctrico== | ||
| + | Una de las herramientas básica en el estudio del problema del potencial eléctrico es el “teorema de existencia y unicidad” que nos dice que la distribución de potencial en un conjunto de conductores en equilibrio electrostático existe y es única. Esto quiere decir que podemos hallarla por cualquier método, incluida la inspiración. Si cumple las condiciones del problema, es la solución, porque no hay otra. | ||
| + | |||
| + | En este problema tenemos un conductor esférico que almacena una carga <math>Q</math>. De este sistema sabemos que: | ||
| + | |||
| + | * El potencial en todos los puntos de la esfera es el mismo, aunque no sabemos cuanto vale | ||
| + | |||
| + | <center><math>V= V_0 \qquad (r < a)</math></center> | ||
| + | |||
| + | * La carga total de la esfera es <math>Q</math>, lo que implica, para cualquier superficie que la rodee | ||
| + | |||
| + | <center><math>\varepsilon_0 \oint \vec{E}\cdot\mathrm{d}\vec{S}= Q</math></center> | ||
| + | |||
| + | * Lejos de la esfera el potencial eléctrico se anula | ||
| + | |||
| + | <center><math>V \to 0\qquad (r\to\infty)</math></center> | ||
| + | |||
| + | * No hay más conductores ni cargas en el sistema. | ||
| + | |||
| + | En principio no podemos suponer que la carga se distribuye uniformemente por la superficie del conductor. Ese no es un dato del problema. | ||
| + | |||
| + | Sin embargo, conocemos un problema concreto que cumple todas las condiciones indicadas: el caso del [[Potencial_eléctrico_debido_a_una_superficie_esférica|potencial debido a una superficie esférica cargada uniformemente]]. | ||
| + | |||
| + | Tal como se ve en la solución de ese problema, el potencial de esa esfera vale | ||
| + | |||
| + | <center><math>V(r)=\begin{cases} \displaystyle \frac{Q}{4\pi\varepsilon_0a} & r \leq a \\ & \\ \displaystyle\frac{Q}{4\pi\varepsilon_0 r} & r > a \end{cases}</math></center> | ||
| + | |||
| + | y por simple comprobación vemos que satisface todas las propiedades del sistema. | ||
| + | |||
| + | Por tanto, esta es la solución del problema. | ||
| + | |||
| + | El campo eléctrico, para este mismo sistema vale | ||
| + | |||
| + | |||
| + | |||
==Voltaje de la esfera== | ==Voltaje de la esfera== | ||
| + | El voltaje de la esfera es el correspondiente a <math>r < a</math> | ||
| + | |||
| + | <center><math>V_0 = \frac{Q}{4\pi\varepsilon_0 a}</math></center> | ||
| + | |||
==Densidad superficial de carga== | ==Densidad superficial de carga== | ||
| + | Puesto que la carga resulta estar distribuida uniformemente, la densidad vale | ||
| + | |||
| + | <center><math>\sigma_s = \frac{Q}{4\pi a^2}</math></center> | ||
==Energía electrostática== | ==Energía electrostática== | ||
| + | ==Caso de voltaje conocido== | ||
[[Categoría:Problemas de electrostática en medios materiales (GIE)]] | [[Categoría:Problemas de electrostática en medios materiales (GIE)]] | ||
Revisión de 21:19 16 may 2012
Contenido |
1 Enunciado
Se tiene una esfera metálica maciza de radio a y no hay más conductores ni cargas en el sistema. Si la esfera almacena una carga total Q calcule:
- el potencial y el campo eléctrico en todos los puntos del espacio.
- el voltaje al que se encuentra
- la densidad superficial de carga.
- la energía electrostática que almacena.
Particularice los resultados anteriores para un radio  y una carga
y una carga 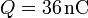 .
.
Suponga ahora que lo que se conoce inicialmente su voltaje V0, pero no su carga. Halle en ese caso la carga que almacena, así como el resto de las cantidades obtenidas anteriormente. Particularice los resultados anteriores para un voltaje 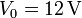 .
.
2 Potencial y campo eléctrico
Una de las herramientas básica en el estudio del problema del potencial eléctrico es el “teorema de existencia y unicidad” que nos dice que la distribución de potencial en un conjunto de conductores en equilibrio electrostático existe y es única. Esto quiere decir que podemos hallarla por cualquier método, incluida la inspiración. Si cumple las condiciones del problema, es la solución, porque no hay otra.
En este problema tenemos un conductor esférico que almacena una carga Q. De este sistema sabemos que:
- El potencial en todos los puntos de la esfera es el mismo, aunque no sabemos cuanto vale

- La carga total de la esfera es Q, lo que implica, para cualquier superficie que la rodee
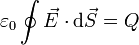
- Lejos de la esfera el potencial eléctrico se anula

- No hay más conductores ni cargas en el sistema.
En principio no podemos suponer que la carga se distribuye uniformemente por la superficie del conductor. Ese no es un dato del problema.
Sin embargo, conocemos un problema concreto que cumple todas las condiciones indicadas: el caso del potencial debido a una superficie esférica cargada uniformemente.
Tal como se ve en la solución de ese problema, el potencial de esa esfera vale
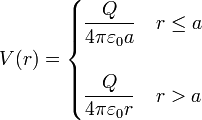
y por simple comprobación vemos que satisface todas las propiedades del sistema.
Por tanto, esta es la solución del problema.
El campo eléctrico, para este mismo sistema vale
3 Voltaje de la esfera
El voltaje de la esfera es el correspondiente a r < a
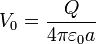
4 Densidad superficial de carga
Puesto que la carga resulta estar distribuida uniformemente, la densidad vale