Entrar Página Discusión Historial Go to the site toolbox

Cuatro placas conductoras paralelas

De Laplace

(Diferencias entre revisiones)
Línea 77: Línea 77:
La nueva capacidad equivalente es
La nueva capacidad equivalente es
-
<center><math>C'_\mathrm{eq}=\left(\frac{1{C_a}+\frac{1}{C_c}\right)^{-1}=0.443\,\mathrm{nF}</math></center>
+
<center><math>C'_\mathrm{eq}=\left(\frac{1}{C_a}+\frac{1}{C_c}\right)^{-1}=0.443\,\mathrm{nF}</math></center>
La carga del condensador equivalente es la misma que la hallada en el apartado anterior, pues la conexión entre las placas se ha hecho tras desconectar la fuente de tensión, por lo que
La carga del condensador equivalente es la misma que la hallada en el apartado anterior, pues la conexión entre las placas se ha hecho tras desconectar la fuente de tensión, por lo que
-
<center><math>Q'_1 = Q_1 = 29.5\,\mathrm{nC}\qquad \qquad Q'_4= -Q'_1=-29.5\,\mathrm{nC}</math></center>
+
<center><math>Q'=Q'_1 = Q_1 = 29.5\,\mathrm{nC}\qquad \qquad Q'_4= -Q'_1=-29.5\,\mathrm{nC}</math></center>
 +
 
 +
Puesto que la placa 2 forma un condensador con el conductor 1, y la 3 lo hace con el 4, tenemos también que
 +
 
 +
<center><math>Q'_2=-Q'_1 = -29.5\,\mathrm{nC}\qquad \qquad Q'_3= -Q'_4=+29.5\,\mathrm{nC}</math></center>
 +
 
 +
Vemos que son iguales y opuestas, como corresponde a que el conjunto de ambas esté descargado.
 +
 
 +
La nueva diferencia de potencial entre las placas extremas la hallamos a partir de esta carga y la nueva capacidad equivalente
 +
 
 +
<center><math>\Delta V' = \frac{Q'}{C'_\mathrm{eq}} = 66.7\,\mathrm{V}</math></center>
 +
 
 +
Si seguimos considerando la placa 4 como la de referencia (tierra)
 +
 
 +
<center><math>V'_1 = 66.7\,\mathrm{V}\qquad\qquad V'_4 = 0\,\mathrm{V}</math></center>
 +
 
 +
Para encontrar el potencial del conductor central, analizamos uno de los dos condensadores
 +
 
 +
<center><math>V'_3 - \overbrace{V_4}^{=0} = \frac{Q'}{C_c}=50\,\mathrm{V}\qquad\Rightarrow\qquad  V'_3=50\,\mathrm{V}</math></center>
 +
 
 +
Resulta el mismo voltaje que antes, pues la carga del tercer condensador y su capacidad no se han visto modificado. Este voltaje es el mismo que el de la placa 2, al estar conectadas.
 +
 
 +
Reuniendo los cuatro resultados queda
 +
 
 +
{| class="bordeado"
 +
|-
 +
!
 +
! 1
 +
! 2
 +
! 3
 +
! 4
 +
|-
 +
! <math>Q'</math> (nC)
 +
| +29.5
 +
| &minus;29.5
 +
| +29.5
 +
| &minus;29.5
 +
|-
 +
! <math>V</math> (V)
 +
| 66.7
 +
| 50.0
 +
| 50.0
 +
| 0.0
 +
|}
 +
 
==Conexión con fuente==
==Conexión con fuente==
[[Categoría:Problemas de electrostática en medios materiales (GIE)]]
[[Categoría:Problemas de electrostática en medios materiales (GIE)]]

Revisión de 15:45 16 may 2012

Contenido

1 Enunciado

Se colocan paralelamente cuatro placas metálicas cuadradas de 20 cm de lado y espesor despreciable, estando la primera separada de la segunda una distancia de 0.2 mm, ésta de la tercera 0.4 mm, y esta de la cuarta 0.6 mm. Las dos placas centrales están aisladas y descargadas. Se coloca la primera placa a 100 V y la última a tierra. Halle el voltaje y la carga de cada placa, así como la energía almacenada.

Sin descargar las placas se desconecta la fuente de tensión. A continuación se conecta por un hilo metálico la segunda con la tercera placa. Halle las nuevas cargas, voltajes y energía almacenada.

¿Cómo cambian los resultados se conectan las placas centrales sin desconectar previamente la fuente de tensión? ¿Qué trabajo realiza la fuente en este caso?

2 Situación inicial

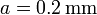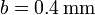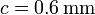Tenemos aquí tres condensadores adyacentes, todos ellos de sección cuadrada y con distancias entre placas a= 0.2\,\mathrm{mm}, b= 0.4\,\mathrm{mm} y c= 0.6\,\mathrm{mm}, respectivamente. La capacidad de cada uno es

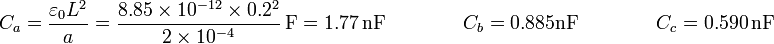
C_a = \frac{\varepsilon_0 L^2}{a}= \frac{8.85\times 10^{-12}\times 0.2^2}{2\times 10^{-4}}\,\mathrm{F}=1.77\,\mathrm{nF}\qquad\qquad C_b = 0.885\mathrm{nF}\qquad\qquad C_c = 0.590\,\mathrm{nF}

En el primer caso, las dos placas están aisladas y descargadas, por lo que los tres condensadores están en serie, siendo la capacidad equivalente

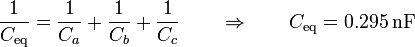
\frac{1}{C_\mathrm{eq}}=\frac{1}{C_a}+\frac{1}{C_b}+\frac{1}{C_c}\qquad\Rightarrow\qquad C_\mathrm{eq} = 0.295\,\mathrm{nF}

Una vez que tenemos la capacidad podemos hallar la carga de la asociación, que es la misma que la de la placa 1

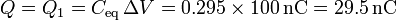
Q=Q_1 = C_\mathrm{eq}\,\Delta V = 0.295\times 100\,\mathrm{nC}=29.5\,\mathrm{nC}

Las placas 2 y 3 están descargadas

Q_2 = Q_3 = 0\,\mathrm{nC}

y la cuarta tiene la carga negativa del condensador equivalente

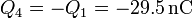
Q_4 = -Q_1 = -29.5\,\mathrm{nC}

Una vez que tenemos las cargas podemos hallar las diferencias de potencial en cada condensador. Empezando por el último

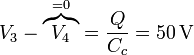
V_3 - \overbrace{V_4}^{=0} = \frac{Q}{C_c}=50\,\mathrm{V}

siguiendo por el central

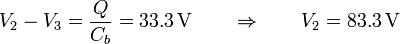
V_2-V_3 = \frac{Q}{C_b}=33.3\,\mathrm{V}\qquad\Rightarrow\qquad V_2 = 83.3\,\mathrm{V}

Reuniendo los cuatro valores

1 2 3 4
Q (nC) 29.5 0.0 0.0 −29.5
V (V) 100.0 83.3 50.0 0.0

La energía almacenada en el sistema es

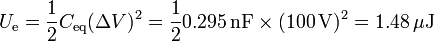
U_\mathrm{e}= \frac{1}{2}C_\mathrm{eq}(\Delta V)^2 = \frac{1}{2}0.295\,\mathrm{nF}\times (100\,\mathrm{V})^2 = 1.48\,\mu\mathrm{J}

3 Conexión sin fuente

Cuando se conectan la placa 2 y la 3, se produce un trasvase de carga de la 2 a la 3 debido a la diferencia de potencial entre ellas. La corriente se detiene una vez que se igualan los voltajes, por lo que tras la conexión

V_2' = V_3'\,

Ahora ya estas placas no están descargadas individualmente, pero sí en conjunto, ya que la carga que sale de una va a parar a la otra

Q_2' + Q_3' = 0\,

En la práctica, esto significa que las dos placas forman ahora un único conductor. En términos del circuito equivalente, la conexión equivale a cortocircuitar el condensador central, reduciendo el sistema a solo dos condensadores, el primero y el tercero.

La nueva capacidad equivalente es

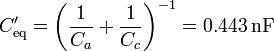
C'_\mathrm{eq}=\left(\frac{1}{C_a}+\frac{1}{C_c}\right)^{-1}=0.443\,\mathrm{nF}

La carga del condensador equivalente es la misma que la hallada en el apartado anterior, pues la conexión entre las placas se ha hecho tras desconectar la fuente de tensión, por lo que

Q'=Q'_1 = Q_1 = 29.5\,\mathrm{nC}\qquad \qquad Q'_4= -Q'_1=-29.5\,\mathrm{nC}

Puesto que la placa 2 forma un condensador con el conductor 1, y la 3 lo hace con el 4, tenemos también que

Q'_2=-Q'_1 = -29.5\,\mathrm{nC}\qquad \qquad Q'_3= -Q'_4=+29.5\,\mathrm{nC}

Vemos que son iguales y opuestas, como corresponde a que el conjunto de ambas esté descargado.

La nueva diferencia de potencial entre las placas extremas la hallamos a partir de esta carga y la nueva capacidad equivalente

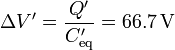
\Delta V' = \frac{Q'}{C'_\mathrm{eq}} = 66.7\,\mathrm{V}

Si seguimos considerando la placa 4 como la de referencia (tierra)

V'_1 = 66.7\,\mathrm{V}\qquad\qquad V'_4 = 0\,\mathrm{V}

Para encontrar el potencial del conductor central, analizamos uno de los dos condensadores

V'_3 - \overbrace{V_4}^{=0} = \frac{Q'}{C_c}=50\,\mathrm{V}\qquad\Rightarrow\qquad V'_3=50\,\mathrm{V}

Resulta el mismo voltaje que antes, pues la carga del tercer condensador y su capacidad no se han visto modificado. Este voltaje es el mismo que el de la placa 2, al estar conectadas.

Reuniendo los cuatro resultados queda

1 2 3 4
Q' (nC) +29.5 −29.5 +29.5 −29.5
V (V) 66.7 50.0 50.0 0.0


4 Conexión con fuente

Obtenido de "http://tesla.us.es/wiki/index.php/Cuatro_placas_conductoras_paralelas"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace