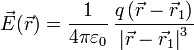Campo de dos cargas
De Laplace
(→Campo eléctrico) |
|||
| Línea 19: | Línea 19: | ||
==Campo eléctrico== | ==Campo eléctrico== | ||
===Introducción=== | ===Introducción=== | ||
| + | El campo eléctrico creado por una carga puntual es de la forma | ||
| + | |||
| + | <center><math>\vec{E}(\vec{r})=\frac{1}{4\pi\varepsilon_0}\,\frac{q}{d^2}\vec{u}</math></center> | ||
| + | |||
| + | siendo <math>q</math> la magnitud de la carga, <math>d</math> la distancia desde el punto de observación a la posición donde se halla la carga y \vec{u} el vector unitario radial en la dirección desde la posición de la carga al punto de observación y con sentido hacia afuera. | ||
| + | |||
| + | Si la carga puntual se encuentra en el punto <math>\vec{r}_1</math> y el punto de observación se halla en <math>\vec{r}</math>, se cumple que | ||
| + | |||
| + | <center><math>d = \left|\vec{r}-\vec{r}_1\right|\qquad\qquad \vec{u}=\frac{\vec{r}-\vec{r}_1}{\left|\vec{r}-\vec{r}_1\right|}</math></center> | ||
| + | |||
| + | lo que da la expresión para el campo | ||
| + | |||
| + | <center><math>\vec{E}(\vec{r})=\frac{1}{4\pi\varepsilon_0}\,\frac{q\left(\vec{r}-\vec{r}_1\right)}{\left|\vec{r}-\vec{r}_1\right|^3}</math></center> | ||
===Punto A=== | ===Punto A=== | ||
===Punto B=== | ===Punto B=== | ||
| Línea 24: | Línea 37: | ||
===Punto D=== | ===Punto D=== | ||
===Resumen=== | ===Resumen=== | ||
| + | |||
==Punto de campo nulo== | ==Punto de campo nulo== | ||
===Punto A=== | ===Punto A=== | ||
Revisión de 12:36 16 abr 2012
Contenido |
1 Enunciado
Se tienen dos cargas q1 y q2 situadas respectivamente en los puntos 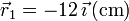 y
y
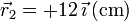 . Halle el campo eléctrico en los puntos
. Halle el campo eléctrico en los puntos
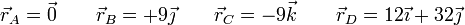
(todas las distancias en cm) para los cuatro casos siguientes
-
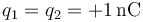
-
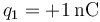 ,
, 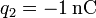
-
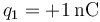 ,
, 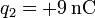
-
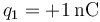 ,
, 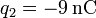
Para los cuatro pares de cargas, localice el punto del eje OX en que se anula el campo eléctrico.
Calcule el potencial eléctrico para todos los casos en todos los puntos indicados.
2 Campo eléctrico
2.1 Introducción
El campo eléctrico creado por una carga puntual es de la forma
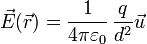
siendo q la magnitud de la carga, d la distancia desde el punto de observación a la posición donde se halla la carga y \vec{u} el vector unitario radial en la dirección desde la posición de la carga al punto de observación y con sentido hacia afuera.
Si la carga puntual se encuentra en el punto 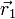 y el punto de observación se halla en
y el punto de observación se halla en  , se cumple que
, se cumple que

lo que da la expresión para el campo