Asociación de cuatro condensadores GIA
De Laplace
(→Solución) |
(→Solución) |
||
| Línea 13: | Línea 13: | ||
<center><math>V_A-V_B=\frac{Q_\mathrm{a}}{C_\mathrm{a}}=\frac{Q_\mathrm{b}}{C_\mathrm{b}}</math></center> | <center><math>V_A-V_B=\frac{Q_\mathrm{a}}{C_\mathrm{a}}=\frac{Q_\mathrm{b}}{C_\mathrm{b}}</math></center> | ||
| + | |||
| + | Fijémonos en las asociación de <math>C_1</math> y <math>C_3</math>: | ||
| + | |||
| + | la capacidad equivalente <math>C_\mathrm{a}</math> es la relación entre la carga eléctrica <math>Q_\mathrm{a}</math> que hay en uno de los conductores no conectados de la asociación y la diferencia de potencial entre éstos, <math>V_A-V_B</math>. Pero el conductor del condensador <math>C_1</math> que no estátanto, la carga <math>Q_\mathrm{a}</math> de | ||
Revisión de 17:59 1 abr 2012
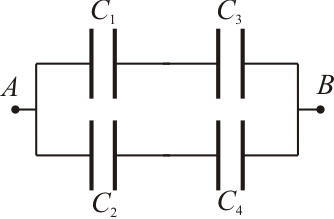
1 Enunciado
, 
, 
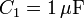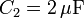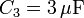y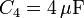 
. La diferencia de potencial entre A y B es de 
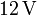. Calcular la carga de cada condensador.
2 Solución
Los condensadores C1 y C3, y por otro lado C2 y C4, forman sendas asociaciones en serie que, a su vez, están conectadas en paralelo, de manera que ambas asociaciones estarán simultáneamente a la misma diferencia de potencial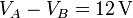 
. Nótese que VA es el valor del potencial en sendos conductores de los condensadores C1 y C2 que son equipotenciales. Análogamente, VB es el potencial de los conductores de los condensadores C3 y C4 que están conectado y tendrán siempre el mismo valor de potencial.
Así, si Ca y Cb son las capcidades equivalentes de las asociaciones C1 y C3, y C2 y C4, respectivamente, se tendrá que:
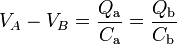
Fijémonos en las asociación de C1 y C3:
la capacidad equivalente Ca es la relación entre la carga eléctrica Qa que hay en uno de los conductores no conectados de la asociación y la diferencia de potencial entre éstos, VA − VB. Pero el conductor del condensador C1 que no estátanto, la carga Qa de
