Ciclo de Stirling (GIE)

De Laplace

(Diferencias entre revisiones)

última version al 15:23 28 mar 2012

Contenido

1 Enunciado
2 Representación gráfica
3 Trabajo y calor
4 Rendimiento
5 Ciclo con regeneración

1 Enunciado

Un Ciclo de Stirling ideal, sin regeneración, está formado por los siguientes pasos:

Inicialmente tenemos 500 cm³ de aire a 300 K y 100 kPa (estado A)

A→B Se comprime el gas de forma isoterma, hasta que se reduce su volumen a 50 cm³

B→C Se calienta el gas hasta una temperatura de 450 K, manteniendo fijado su volumen.

C→D Se expande el gas a temperatura constante hasta que vuelve a su volumen inicial.

D→A Se enfría el gas manteniendo constante su volumen hasta que su temperatura vuelve a ser la inicial

Para este ciclo.

Indique gráficamente como sería en un diagrama pV.
Calcule el trabajo y el calor que entran en el sistema en cada uno de los cuatro pasos.
Calcule el rendimiento del ciclo.

En un ciclo de Stirling con regeneración, el calor liberado en el proceso D\→A no se pierde sino que se emplea para efectuar el calentamiento en B→C

Calcule el rendimiento del ciclo de Stirling con regeneración. ¿Es mayor o menor que el de una máquina de Carnot que opere entre las mismas temperaturas?

2 Representación gráfica

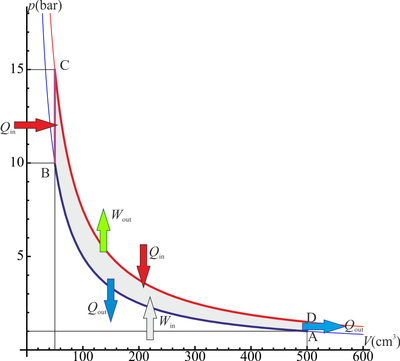
El proceso se compone de cuatro pasos, cuya representación gráfica en un diagrama pV es la siguiente:

A→B Se comprime el gas de forma isoterma, hasta que se reduce su volumen a 50 cm³. Esto corresponde a un tramo de hipérbola correspondiente a la temperatura indicada.

B→C Se calienta el gas hasta una temperatura de 450 K, manteniendo fijado su volumen. Gráficamente, es una línea vertical entre las dos isotermas.

C→D Se expande el gas a temperatura constante hasta que vuelve a su volumen inicial. Otro arco de hipérbola ahora recorrido hacia volúmenes crecientes.

D→A Se enfría el gas manteniendo constante su volumen hasta que su temperatura vuelve a ser la inicial. Es un tramo vertical hacia abajo, cerrando el ciclo.

Los valores de las presiones, temperaturas y volúmenes de cada vértice del ciclo son los siguientes. Partimos del estado A, de cual conocemos las tres magnitudes

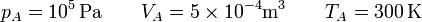
$p_A = 10^5\,\mathrm{Pa}\qquad V_A = 5\times 10^{-4}\mathrm{m}^3\qquad T_A = 300\,\mathrm{K}$

En el estado B tenemos la temperatura y el volumen

$T_B = T_A=300\,\mathrm{K} \qquad V_B = 5\times 10^{-5}\mathrm{m}^3$

y por la ley de los gases ideales hallamos la presión

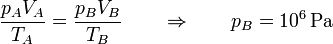
$\frac{p_AV_A}{T_A}=\frac{p_BV_B}{T_B}\qquad\Rightarrow\qquad p_B = 10^6\,\mathrm{Pa}$

A temperatura constante, si el volumen se divide por 10, la presión se multiplica por el mismo factor.

En el estado C de nuevo tenemos la temperatura y el volumen

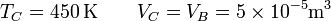
$T_C = 450\,\mathrm{K} \qquad V_C = V_B = 5\times 10^{-5}\mathrm{m}^3$

y hallamos la presión del mismo modo

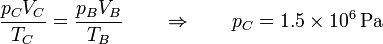
$\frac{p_CV_C}{T_C}=\frac{p_BV_B}{T_B}\qquad\Rightarrow\qquad p_C = 1.5\times 10^6\,\mathrm{Pa}$

En este caso la temperatura se multiplica por un factor 1.5 y lo mismo ocurre con la presión.

En el último vértice de nuevo tenemos la temperatura y el volumen

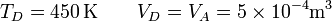
$T_D = 450\,\mathrm{K} \qquad V_D = V_A = 5\times 10^{-4}\mathrm{m}^3$

y resulta la presión

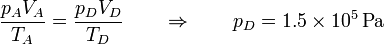
$\frac{p_AV_A}{T_A}=\frac{p_DV_D}{T_D}\qquad\Rightarrow\qquad p_D = 1.5\times 10^5\,\mathrm{Pa}$

Podemos recoger estos estados en la siguiente tabla:

Estado	$p (kPa)$	$V (cm 3)$	$T (K)$
A	100	500	300
B	1000	50	300
C	1500	50	450
D	150	500	450

3 Trabajo y calor

Para cada uno de los cuatro pasos tenemos los siguientes valores del trabajo, calor y la variación de energía interna:

3.1 Compresión isoterma

En el paso A→B la temperatura del aire no cambia y por tanto su energía interna permanece constante

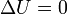
$\Delta U=0\,$

El trabajo es el correspondiente a una compresión cuasiestática a temperatura constante

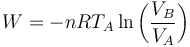
$W = -n RT_A\ln\left(\frac{V_B}{V_A}\right)$

En términos de los datos del problema

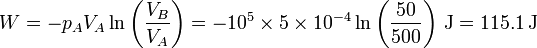
$W = -p_AV_A\ln\left(\frac{V_B}{V_A}\right)= -10^5\times 5\times 10^{-4}\ln\left(\frac{50}{500}\right)\,\mathrm{J}=115.1\,\mathrm{J}$

Puesto que la energía interna no varía el calor es igual al trabajo cambiado de signo

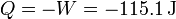
$Q = -W = -115.1\,\mathrm{J}$

3.2 Calentamiento isócoro

En el paso B→C, el volumen no cambia y por tanto no se realiza trabajo sobre el gas.

$W=0\,$

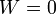
La variación en la energía interna es proporcional al incremento de temperaturas

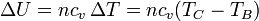
$\Delta U = nc_v\,\Delta T = nc_v(T_C-T_B)$

cuyo valor numérico es

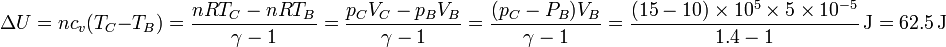
$\Delta U = nc_v(T_C-T_B)= \frac{nRT_C-nRT_B}{\gamma-1}=\frac{p_CV_C-p_BV_B}{\gamma-1}=\frac{(p_C-P_B)V_B}{\gamma-1}=\frac{(15-10)\times 10^5\times 5\times 10^{-5}}{1.4-1}\,\mathrm{J}=62.5\,\mathrm{J}$

y por el primer principio de la termodinámica, el calor será igual a esta cantidad

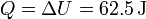
$Q = \Delta U = 62.5\,\mathrm{J}$

3.3 Expansión isoterma

En el paso C→D la temperatura del aire vuelve a ser constante y por tanto su energía interna no cambia

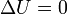
$\Delta U=0\,$

El trabajo es el de una expansión cuasiestática a temperatura constante

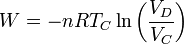
$W = -n RT_C\ln\left(\frac{V_D}{V_C}\right)$

cuyo valor numérico es

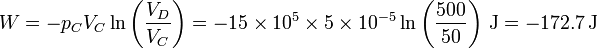
$W = -p_CV_C\ln\left(\frac{V_D}{V_C}\right)= -15\times 10^5\times 5\times 10^{-5}\ln\left(\frac{500}{50}\right)\,\mathrm{J}=-172.7\,\mathrm{J}$

Puesto que la energía interna no varía el calor es igual al trabajo cambiado de signo

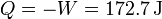
$Q = -W = 172.7\,\mathrm{J}$

3.4 Enfriamiento isócoro

Por último, en el paso D→A, el volumen no cambia y el trabajo sobre el gas es nulo.

$W=0\,$

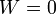
La variación en la energía interna es proporcional al incremento de temperaturas

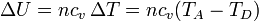
$\Delta U = nc_v\,\Delta T = nc_v(T_A-T_D)$

cuyo valor numérico es el mismo que en el calentamiento, pero cambiado de signo

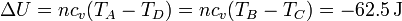
$\Delta U = nc_v(T_A-T_D)= nc_v(T_B-T_C) = -62.5\,\mathrm{J}$

y el calor es igual a esta cantidad

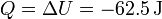
$Q = \Delta U = -62.5\,\mathrm{J}$

3.5 Resumen

Reuniendo todos los resultados

Proceso	$Q (J)$	$W (J)$	$Δ U (J)$
A→B	-115.1	+115.1	0
B→C	+62.5	0	+62.5
C→D	+172.7	-172.7	0
D→A	-62.5	0	-62.5

4 Rendimiento

En este proceso se absorbe calor en al calentamiento isócoro y la expansión isoterma, y se cede en los otros dos procesos. El valor neto del calor absorbido es

$Q_\mathrm{in}=Q_{B\to C}+Q_{C\to D}=nc_v(T_C-T_B)+nRT_C\ln\left(\frac{V_D}{V_C}\right)= \left(172.7+62.5\right)\mathrm{J}=235.2\,\mathrm{J}$

y del cedido

$Q_\mathrm{out}=\left|nc_v(T_A-T_B)+nRT_A\ln\left(\frac{V_B}{V_A}\right)\right|=\left(115.1+62.5\right)\mathrm{J}=177.6\,\mathrm{J}$

de forma que el rendimiento es

$\eta = 1 -\frac{Q_\mathrm{out}}{Q_\mathrm{in}}= 1- \frac{c_v(T_C-T_F) + RT_F\ln(r)}{c_v(T_C-T_F)+RT_C\ln(r)}$

siendo

$T_C = T_D\qquad\qquad T_F = T_A=T_B\qquad\qquad r = \frac{V_A}{V_B}=\frac{V_D}{V_C}$

El valor numérico de este rendimiento es

$\eta = 1-\frac{177.6}{235.2} = 24.5\%$

Podemos comprobar que este rendimiento es siempre menor que el de una máquina reversible que opere entre estas dos temperaturas

$\eta_\mathrm{rev}=1-\frac{T_F}{T_C}$

siendo el rendimiento de la segunda ley

$\epsilon= \frac{\eta}{\eta^\mathrm{rev}}=\frac{R T_C\ln(r)}{c_v(T_C-T_F)+R T_C\ln(r)} < 1$

(ya que el denominador es mayor que el numerador). En nuestro caso

$\eta^\mathrm{rev} = 1-\frac{300}{450}=33.3\%$

y

$\epsilon = \frac{24.5}{33.3}= 73.5\%$

5 Ciclo con regeneración

Si el calor del enfriamiento no es desperdiciado, sino que se reutiliza en el calentamiento isócoro (lo cual es teóricamente posible, ya que al pasar por las mismas temperaturas se trata de una transferencia reversible), entonces el único calor que entra en el sistema es

$Q_\mathrm{in}=Q_{C\to D}=nRT_C\ln(r) = 172.7\,\mathrm{J}$

y el único que sale

$Q_\mathrm{in}=\left|Q_{A\to B}=nRT_F\ln(r)\right| = 115.1\,\mathrm{J}$

siendo el rendimiento

$\eta = 1-\frac{nRT_F\ln(r)}{nRT_C\ln(r)}=1-\frac{T_F}{T_C}$

que es el mismo de una máquina de Carnot que opere entre las dos temperaturas. En este caso, entonces

$\eta = \eta^\mathrm{rev} = 33.3\% \qquad\Rightarrow\qquad \epsilon = \frac{\eta}{\eta^\mathrm{rev}}=100\%$

Un ciclo ideal de Stirling con regeneración es un ciclo completamente reversible y por tanto su rendimiento es el máximo posible.

@@ Línea 18: / Línea 18: @@
 ==Representación gráfica==
-<center>[[Archivo:EsquemaMotorStirling.gif]]</center>
-<center>[[Archivo:EsquemaMotorStirling02.gif]]{{qquad}}{{qquad}}[[Archivo:EsquemaMotorStirling03.gif]]</center>
 [[Archivo:ciclo-stirling-02.png|400px|right]]
@@ Línea 96: / Línea 91: @@
 ==Trabajo y calor==
+[[Archivo:ciclo-stirling.gif|right]]
 Para cada uno de los cuatro pasos tenemos los siguientes valores del trabajo, calor y la variación de energía interna:
@@ Línea 131: / Línea 128: @@
 <center><math>Q = \Delta U = 62.5\,\mathrm{J}</math></center>
+===Expansión isoterma===
+En el paso C&rarr;D la temperatura del aire vuelve a ser constante y por tanto su energía interna no cambia
+<center><math>\Delta U=0\,</math></center>
+El trabajo es el de una expansión cuasiestática a temperatura constante
+<center><math>W = -n RT_C\ln\left(\frac{V_D}{V_C}\right)</math></center>
+cuyo valor numérico es
+<center><math>W = -p_CV_C\ln\left(\frac{V_D}{V_C}\right)= -15\times 10^5\times 5\times 10^{-5}\ln\left(\frac{500}{50}\right)\,\mathrm{J}=-172.7\,\mathrm{J}</math></center>
+Puesto que la energía interna no varía el calor es igual al trabajo cambiado de signo
+<center><math>Q = -W = 172.7\,\mathrm{J}</math></center>
+===Enfriamiento isócoro===
+Por último, en el paso D&rarr;A, el volumen no cambia y el trabajo sobre el gas es nulo.
+<center><math>W=0\,</math></center>
+La variación en la energía interna es proporcional al incremento de temperaturas
+<center><math>\Delta U = nc_v\,\Delta T = nc_v(T_A-T_D)</math></center>
+cuyo valor numérico es el mismo que en el calentamiento, pero cambiado de signo
+<center><math>\Delta U = nc_v(T_A-T_D)= nc_v(T_B-T_C) = -62.5\,\mathrm{J}</math></center>
+y el calor es igual a esta cantidad
+<center><math>Q = \Delta U = -62.5\,\mathrm{J}</math></center>
+===Resumen===
+Reuniendo todos los resultados
+{| class="bordeado"
+|-
+! Proceso
+! <math>Q (\mathrm{J})</math>
+! <math>W (\mathrm{J})</math>
+! <math>\Delta U (\mathrm{J})</math>
+|-
+| A&rarr;B
+| -115.1
+| +115.1
+| 0
+|-
+| B&rarr;C
+| +62.5
+| 0
+| +62.5
+|-
+| C&rarr;D
+| +172.7
+| -172.7
+| 0
+|-
+| D&rarr;A
+| -62.5
+| 0
+| -62.5
+|}
 ==Rendimiento==
 En este proceso se absorbe calor en al calentamiento isócoro y la expansión isoterma, y se cede en los otros dos procesos. El valor neto del calor absorbido es
-<center><math>|Q_c|=nc_v(T2-T1)+nRT_2\ln\left(\frac{V_A}{V_B}\right)</math></center>
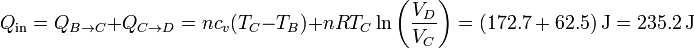
+<center><math>Q_\mathrm{in}=Q_{B\to C}+Q_{C\to D}=nc_v(T_C-T_B)+nRT_C\ln\left(\frac{V_D}{V_C}\right)= \left(172.7+62.5\right)\mathrm{J}=235.2\,\mathrm{J}</math></center>
 y del cedido
-<center><math>|Q_f|=nc_v(T2-T1)+nRT_1\ln\left(\frac{V_A}{V_B}\right)</math></center>
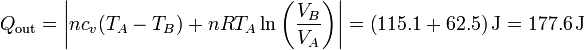
+<center><math>Q_\mathrm{out}=\left|nc_v(T_A-T_B)+nRT_A\ln\left(\frac{V_B}{V_A}\right)\right|=\left(115.1+62.5\right)\mathrm{J}=177.6\,\mathrm{J}</math></center>
 de forma que el rendimiento es
-<center><math>\eta = 1 -\frac{|Q_f|}{|Q_c|}= 1- \frac{c_v(T_2-T_1) + RT_1\ln(r)}{c_v(T_2-T_1)+RT_2\ln(r)}</math></center>
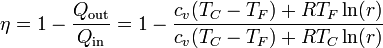
+<center><math>\eta = 1 -\frac{Q_\mathrm{out}}{Q_\mathrm{in}}= 1- \frac{c_v(T_C-T_F) + RT_F\ln(r)}{c_v(T_C-T_F)+RT_C\ln(r)}</math></center>
-siendo <math>r</math> la relación de compresión.
+siendo
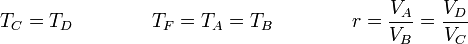
+<center><math>T_C = T_D\qquad\qquad T_F = T_A=T_B\qquad\qquad r = \frac{V_A}{V_B}=\frac{V_D}{V_C}</math></center>
+El valor numérico de este rendimiento es
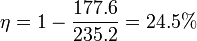
+<center><math>\eta = 1-\frac{177.6}{235.2} = 24.5\%</math></center>
 Podemos comprobar que este rendimiento es siempre menor que el de una máquina reversible que opere entre estas dos temperaturas
-<center><math>\eta_\mathrm{max}=1-\frac{T_1}{T_2}</math></center>
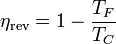
+<center><math>\eta_\mathrm{rev}=1-\frac{T_F}{T_C}</math></center>
-siendo la diferencia
+siendo el rendimiento de la segunda ley
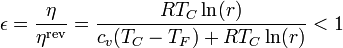
+<center><math>\epsilon= \frac{\eta}{\eta^\mathrm{rev}}=\frac{R T_C\ln(r)}{c_v(T_C-T_F)+R T_C\ln(r)} < 1</math></center>
+(ya que el denominador es mayor que el numerador). En nuestro caso
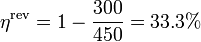
+<center><math>\eta^\mathrm{rev} = 1-\frac{300}{450}=33.3\%</math></center>
+y
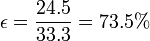
+<center><math>\epsilon = \frac{24.5}{33.3}= 73.5\%</math></center>
 ==Ciclo con regeneración==
+Si el calor del enfriamiento no es desperdiciado, sino que se reutiliza en el calentamiento isócoro (lo cual es teóricamente posible, ya que al pasar por las mismas temperaturas se trata de una transferencia reversible), entonces el único calor que entra en el sistema es
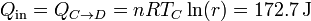
+<center><math>Q_\mathrm{in}=Q_{C\to D}=nRT_C\ln(r) = 172.7\,\mathrm{J}</math></center>
+y el único que sale
+<center><math>Q_\mathrm{in}=\left|Q_{A\to B}=nRT_F\ln(r)\right| = 115.1\,\mathrm{J}</math></center>
+siendo el rendimiento
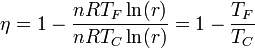
+<center><math>\eta = 1-\frac{nRT_F\ln(r)}{nRT_C\ln(r)}=1-\frac{T_F}{T_C}</math></center>
+que es el mismo de una máquina de Carnot que opere entre las dos temperaturas. En este caso, entonces
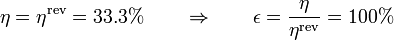
+<center><math>\eta = \eta^\mathrm{rev} = 33.3\% \qquad\Rightarrow\qquad \epsilon = \frac{\eta}{\eta^\mathrm{rev}}=100\%</math></center>
+Un ciclo ideal de Stirling con regeneración es un ciclo completamente reversible y por tanto su rendimiento es el máximo posible.
 [[Categoría:Problemas de máquinas térmicas (GIE)]]

Ciclo de Stirling (GIE)

De Laplace

última version al 15:23 28 mar 2012

Contenido

1 Enunciado

2 Representación gráfica

3 Trabajo y calor

3.1 Compresión isoterma

3.2 Calentamiento isócoro

3.3 Expansión isoterma

3.4 Enfriamiento isócoro

3.5 Resumen

4 Rendimiento

5 Ciclo con regeneración

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES