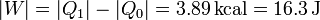Transferencia reversible de calor
De Laplace
(→Temperatura final) |
(→Calor intercambiado) |
||
| (9 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| - | Se tienen dos recipientes adiabáticos conteniendo 500 g de agua cada uno, a 0°C y 100°C | + | Se tienen dos recipientes adiabáticos conteniendo 500 g de agua cada uno, a 0°C y 100°C respectivamente. |
# Se ponen en contacto a través de una pared diaterma. Halle: | # Se ponen en contacto a través de una pared diaterma. Halle: | ||
| Línea 33: | Línea 33: | ||
Sustituyendo los valores numéricos | Sustituyendo los valores numéricos | ||
| - | <center><math>\Delta S = 500 \ln\left(\frac{323^2}{273\ | + | <center><math>\Delta S = 500 \ln\left(\frac{323.15^2}{273.15\cdot 373.15}\right)\,\frac{\mathrm{cal}}{\mathrm{K}} = 12.13\,\frac{\mathrm{cal}}{\mathrm{K}}</math></center> |
Esa variación es positiva, lo que indica que el proceso es posible e irreversible. | Esa variación es positiva, lo que indica que el proceso es posible e irreversible. | ||
| Línea 41: | Línea 41: | ||
Lo que caracteriza a un conjunto de procesos reversibles es que en cada uno de ellos la variación de entropía es nula. Por ello, la ecuación que permite calcular la temperatura final es | Lo que caracteriza a un conjunto de procesos reversibles es que en cada uno de ellos la variación de entropía es nula. Por ello, la ecuación que permite calcular la temperatura final es | ||
| - | 0 = \Delta S = | + | <center><math> |
| + | 0 = \Delta S = \Delta S_1 + \Delta S_2 = mc\ln\left(\frac{T_f}{T_1}\right)+ mc\ln\left(\frac{T_f}{T_0}\right) = mc\ln\left(\frac{T_f^2}{T_0T_1}\right)</math></center> | ||
| + | |||
| + | y la temperatura final resulta ser la media geométrica de las dos temperaturas intermedias (antes era la media aritmética) | ||
| + | |||
| + | <center><math>T_f = \sqrt{T_0T_1} = 319.26\,\mathrm{K} = 46.11^\circ\mathrm{C}</math></center> | ||
| + | |||
| + | Esta temperatura es inferior a la calculada anteriormente porque en un proceso reversible no todo el calor del foco caliente va a parar al frío, sino que parte se emplea en producir trabajo. | ||
===Calor intercambiado=== | ===Calor intercambiado=== | ||
| + | El calor cedido por el foco caliente es | ||
| + | |||
| + | <center><math>Q_1 = mc(T_f-T_1) = 500(46.1-100.0)\,\mathrm{cal}=-26.9\,\mathrm{kcal}</math></center> | ||
| + | |||
| + | y el calor absorbido por el foco frío | ||
| + | |||
| + | <center><math>Q_0 = mc(T_f-T_0) = 500(46.1-0.0)\,\mathrm{cal} = +23.1\,\mathrm{kcal}</math></center> | ||
| + | |||
===Trabajo realizado=== | ===Trabajo realizado=== | ||
| + | El trabajo realizado en este proceso es la diferencia entre el calor cedido y el absorbido | ||
| + | |||
| + | <center><math>|W| = |Q_1|-|Q_0| = 3.89\,\mathrm{kcal} = 16.3\,\mathrm{J}</math></center> | ||
[[Categoría: Problemas del segundo principio de la termodinámica]] | [[Categoría: Problemas del segundo principio de la termodinámica]] | ||
última version al 20:58 21 mar 2012
Contenido |
1 Enunciado
Se tienen dos recipientes adiabáticos conteniendo 500 g de agua cada uno, a 0°C y 100°C respectivamente.
- Se ponen en contacto a través de una pared diaterma. Halle:
- La temperatura final del agua.
- La cantidad de calor transferida.
- La variación de entropía en el proceso.
- Suponga ahora que el contacto térmico no se hace directamente sino a través de una máquina térmica reversible que usa los recipientes como foco caliente y foco frío. Teniendo en cuenta que todos los procesos son reversibles
- Halle la temperatura final del agua
- Calcule el calor cedido por el agua caliente y el absorbido por el agua fría
- Determine el trabajo que se puede extraer del sistema.
2 Contacto directo
En el primer proceso tenemos una transferencia de calor del foco caliente al foco frío sin producción alguna de trabajo. Todo el calor que cede el foco caliente lo absorbe el foco frío.
2.1 Temperatura final
Puesto que el único intercambio de calor es interno



2.2 Calor transferido
El calor que cede el foco caliente es
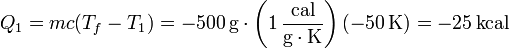
Este calor es negativo puesto que sale del sistema. la misma cantidad de calor entra en el foco frío.
2.3 Variación de entropía
La variación de entropía será la suma de lo que cambia la del agua aclaiente más lo que lo hace la del agua fría. El resultado es
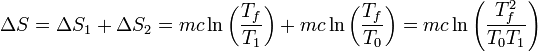
Sustituyendo los valores numéricos
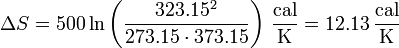
Esa variación es positiva, lo que indica que el proceso es posible e irreversible.
3 Contacto reversible
3.1 Temperatura final
Lo que caracteriza a un conjunto de procesos reversibles es que en cada uno de ellos la variación de entropía es nula. Por ello, la ecuación que permite calcular la temperatura final es
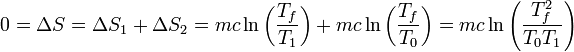
y la temperatura final resulta ser la media geométrica de las dos temperaturas intermedias (antes era la media aritmética)
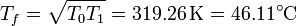
Esta temperatura es inferior a la calculada anteriormente porque en un proceso reversible no todo el calor del foco caliente va a parar al frío, sino que parte se emplea en producir trabajo.
3.2 Calor intercambiado
El calor cedido por el foco caliente es
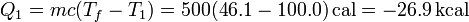
y el calor absorbido por el foco frío
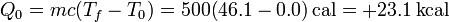
3.3 Trabajo realizado
El trabajo realizado en este proceso es la diferencia entre el calor cedido y el absorbido