Diseño de una clepsidra
De Laplace
(→Solución) |
(→Enunciado) |
||
| (9 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| - | Una clepsidra es un reloj de agua, usado en tiempos antiguos para medir el tiempo. Un modelo simple consiste en un recipiente abierto al aire en su parte superior, con un agujero de | + | Una clepsidra es un reloj de agua, usado en tiempos antiguos para medir el tiempo. Un modelo simple consiste en un recipiente abierto al aire en su parte superior, con un agujero de pequeña sección en el fondo. El recipiente se llena de agua y esta fluye por el agujero. La variación del nivel de agua en el recipiente indica el paso del tiempo. Para poder usar una escala equiespaciada es conveniente que la velocidad con que baja el nivel de agua sea constante. Si la forma del recipiente es de un volumen de revolución, de modo que para cada altura su sección es un círculo de radio <math>r(y)</math>, y el radio del orificio de salida es <math>r_0</math>, encuentra el perfil de la curva que consigue que la velocidad con que desciende el nivel de agua sea constante. |
==Solución== | ==Solución== | ||
| Línea 9: | Línea 9: | ||
Podemos relacionar la variación del nivel con el flujo a través del orificio observando que la cantidad de agua que disminuye por arriba en un intervalo <math>\mathrm{d}t</math> coincide con la que sale por el orificio en el mismo intervalo. Esto nos da la ecuación de continuidad | Podemos relacionar la variación del nivel con el flujo a través del orificio observando que la cantidad de agua que disminuye por arriba en un intervalo <math>\mathrm{d}t</math> coincide con la que sale por el orificio en el mismo intervalo. Esto nos da la ecuación de continuidad | ||
| - | <center><math>v(y)A(y) = v(0)A_0</math></center> | + | <center><math>v(y)A(y) = v(0)A_0\,</math></center> |
En el extremo superior, el área es la de un círculo de radio <math>r(y)</math> y la velocidad coincide con la de bajada del nivel, por lo que | En el extremo superior, el área es la de un círculo de radio <math>r(y)</math> y la velocidad coincide con la de bajada del nivel, por lo que | ||
| - | <center><math>v(y)A(y) = \dot{y}\pi r(y) | + | <center><math>v(y)A(y) = \dot{y}\pi r</math>{{qquad}}{{qquad}}<math>r=r(y)\,</math></center> |
En el extremo inferior el área es la del orificio, | En el extremo inferior el área es la del orificio, | ||
| Línea 29: | Línea 29: | ||
Combinando todo esto nos queda | Combinando todo esto nos queda | ||
| - | <center><math>\dot{y}\pi r | + | <center><math>\dot{y}\pi r^2 = \pi r_0^2 \sqrt{2gy}</math>{{tose}} <math>\dot{y}=\frac{r_0^2\sqrt{2gy}}{r^2}</math></center> |
Este nivel descenderá a ritmo constante si | Este nivel descenderá a ritmo constante si | ||
| - | <center><math>\frac{r_0^2\sqrt{2gy}}{r | + | <center><math>\frac{r_0^2\sqrt{2gy}}{r^2} = k</math>{{tose}} <math>r=r(y) = \frac{r_0(2g)^{1/4}}{\sqrt{k}} y^{1/4} = C y^{1/4}</math></center> |
o, invirtiendo esta relación, obtenemos la cuártica | o, invirtiendo esta relación, obtenemos la cuártica | ||
| Línea 45: | Línea 45: | ||
y la ecuación de Bernoulli nos da la ecuación | y la ecuación de Bernoulli nos da la ecuación | ||
| - | <center><math>\dot{y}=\frac{r_0^2\sqrt{\dot{y}^2+2gy}}{r | + | <center><math>\dot{y}=\frac{r_0^2\sqrt{\dot{y}^2+2gy}}{r^2}</math></center> |
y si el ritmo de bajada es constante | y si el ritmo de bajada es constante | ||
| Línea 55: | Línea 55: | ||
<center><math>y = \frac{k^2(r^4-r_0^4)}{2gr_0^4 }</math></center> | <center><math>y = \frac{k^2(r^4-r_0^4)}{2gr_0^4 }</math></center> | ||
| - | [[Imagen:perfil_clepsidra.gif| | + | [[Imagen:perfil_clepsidra.gif|left]] |
| - | Como caso | + | Como caso concreto, supongamos que queremos una clepsidra que se vacíe en una hora exacta y que tenga un orificio de 1 mm de radio y una altura de 20 cm. En este caso |
| - | <center><math>k = \frac{0.2\,\mathrm{m}}{3600\,\mathrm{s}}= | + | <center><math>k = \frac{0.2\,\mathrm{m}}{3600\,\mathrm{s}}=55.6\times 10^{-6}\frac{\mathrm{m}}{\mathrm{s}}</math></center> |
resulta la ecuación | resulta la ecuación | ||
| - | <center><math>r(y) = 0.282365 (1.5731\times 10^-10 + y)^{1/4}\qquad (SI)</math></center> | + | <center><math>r(y) = 0.282365 (1.5731\times 10^{-10} + y)^{1/4}\simeq 0.282 y^{1/4}\qquad \mbox{(SI)}</math></center> |
| + | |||
| + | [[Imagen:clepsidra_3d.gif|right]] | ||
| + | |||
| + | En las figuras vemos el perfil y como sería su forma tridimensional. | ||
| + | |||
| + | El radio máximo será para y = 20 cm = 0.2 m, para el cual | ||
| + | |||
| + | <center><math>r_\mathrm{max}= 0.189\,\mathrm{m}=18.9\,\mathrm{cm}</math></center> | ||
| + | |||
| + | Dado que este radio es mucho mayor que el del orificio, está completamente justificado el despreciar la velocidad de bajada del nivel frente a la de salida del orificio. Concretamente, la velocidad de salida en el instante inicial sería | ||
| + | |||
| + | <center><math>v(0)\simeq \sqrt{2gh}=1.98\,\frac{\mathrm{m}}{\mathrm{s}}</math></center> | ||
| + | |||
| + | que es más de 20 millones de veces superior a la de descenso del nivel. | ||
| + | |||
[[Categoría:Problemas de introducción a la mecánica de fluidos]] | [[Categoría:Problemas de introducción a la mecánica de fluidos]] | ||
última version al 18:46 17 mar 2012
1 Enunciado
Una clepsidra es un reloj de agua, usado en tiempos antiguos para medir el tiempo. Un modelo simple consiste en un recipiente abierto al aire en su parte superior, con un agujero de pequeña sección en el fondo. El recipiente se llena de agua y esta fluye por el agujero. La variación del nivel de agua en el recipiente indica el paso del tiempo. Para poder usar una escala equiespaciada es conveniente que la velocidad con que baja el nivel de agua sea constante. Si la forma del recipiente es de un volumen de revolución, de modo que para cada altura su sección es un círculo de radio r(y), y el radio del orificio de salida es r0, encuentra el perfil de la curva que consigue que la velocidad con que desciende el nivel de agua sea constante.
2 Solución
Se trata de que el nivel descienda a ritmo constante, esto es, hay que buscar una curva r(y) tal que
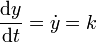
Podemos relacionar la variación del nivel con el flujo a través del orificio observando que la cantidad de agua que disminuye por arriba en un intervalo dt coincide con la que sale por el orificio en el mismo intervalo. Esto nos da la ecuación de continuidad
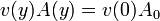
En el extremo superior, el área es la de un círculo de radio r(y) y la velocidad coincide con la de bajada del nivel, por lo que
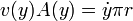
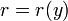
En el extremo inferior el área es la del orificio,
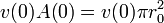
La velocidad de salida por el orificio la obtenemos por la ley de Bernoulli

La presión tanto arriba como abajo es la atmosférica, por estar abierto al exterior. Si consideramos despreciable la velocidad en el nivel superior frente a la de salida, obtenemos la relación aproximada
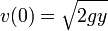
Combinando todo esto nos queda
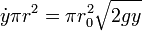

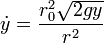
Este nivel descenderá a ritmo constante si


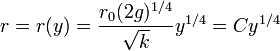
o, invirtiendo esta relación, obtenemos la cuártica
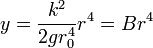
Si la velocidad de bajada del nivel no es despreciable frente a la de salida, refinamos el cálculo. En ese caso tenemos
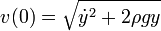
y la ecuación de Bernoulli nos da la ecuación
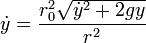
y si el ritmo de bajada es constante
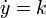

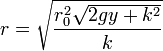
que invertida nos da la cuártica
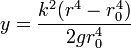
Como caso concreto, supongamos que queremos una clepsidra que se vacíe en una hora exacta y que tenga un orificio de 1 mm de radio y una altura de 20 cm. En este caso

resulta la ecuación
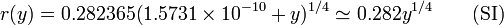
En las figuras vemos el perfil y como sería su forma tridimensional.
El radio máximo será para y = 20 cm = 0.2 m, para el cual
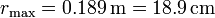
Dado que este radio es mucho mayor que el del orificio, está completamente justificado el despreciar la velocidad de bajada del nivel frente a la de salida del orificio. Concretamente, la velocidad de salida en el instante inicial sería
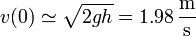
que es más de 20 millones de veces superior a la de descenso del nivel.







