Esfera conductora hueca con carga puntual GIA
De Laplace
(Diferencias entre revisiones)
(→Solución) |
(→Solución) |
||
| Línea 5: | Línea 5: | ||
==Solución== | ==Solución== | ||
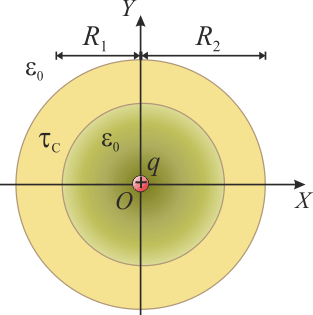
| - | En la figura se muestra una sección transversal del sistema bajo estudio. Se trata de una esfera conductora de radio <math>R_2</math>, descargada y aislada, en cuyo interior hay un hueco esférico y concéntrico de radio <math>R_1</math>, que se encuentra vacío salvo en su centro <math>O</math>, donde hay situada una carga puntual de valor <math>q</math>. Ésta carga produce una campo eléctrico radial con centro en la carga (es decir, en el punto <math>O</math>), | + | En la figura se muestra una sección transversal del sistema bajo estudio. Se trata de una esfera conductora de radio <math>R_2</math>, descargada y aislada, en cuyo interior hay un hueco esférico y concéntrico de radio <math>R_1</math>, que se encuentra vacío salvo en su centro <math>O</math>, donde hay situada una carga puntual de valor <math>q</math>, que supondremos positiva. Ésta carga produce una campo eléctrico radial con centro en la carga (es decir, en el punto <math>O</math>), |
| - | <center><math>\mathbf{E}_q(\mathbf{r})=k_e\!\ q \ \frac{\mathbf{r}}{|\mathbf{r}|^3}\ =\frac{k_e\!\ q}{r^2}\ \mathbf{u}_r\,\mathrm{con}\;\;\overrightarrow{OP}=\mathbf{r}=r\!\ \mathbf{u}_r</math></center> | + | <center><math>\mathbf{E}_q(\mathbf{r})=k_e\!\ q \ \frac{\mathbf{r}}{|\mathbf{r}|^3}\ =\frac{k_e\!\ q}{r^2}\ \mathbf{u}_r\,\mathrm{,}\;\;\;\mathrm{con}\;\;\overrightarrow{OP}=\mathbf{r}=r\!\ \mathbf{u}_r</math></center> |
| - | + | definido en todos los puntos del espacio. Si la carga puntual se encuentra en el hueco del conductor ideal. | |
| - | + | ||
Revisión de 18:19 16 mar 2012
1 Enunciado
2 Solución
En la figura se muestra una sección transversal del sistema bajo estudio. Se trata de una esfera conductora de radio R2, descargada y aislada, en cuyo interior hay un hueco esférico y concéntrico de radio R1, que se encuentra vacío salvo en su centro O, donde hay situada una carga puntual de valor q, que supondremos positiva. Ésta carga produce una campo eléctrico radial con centro en la carga (es decir, en el punto O),
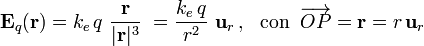
definido en todos los puntos del espacio. Si la carga puntual se encuentra en el hueco del conductor ideal.
