Entrar Página Discusión Historial Go to the site toolbox

Campo eléctrico entre dos cargas puntuales GIA

De Laplace

(Diferencias entre revisiones)
(Página creada con '== Enunciado == Se tienen dos cargas puntuales <math>q_1</math> y <math>q_2</math> separadas por una distancia <math>d</math>. Determina el punto sobre la línea que las une en…')
(→Enunciado)
 
(Una edición intermedia no se muestra.)
Línea 5: Línea 5:
# <math>q_1=q,\quad q_2=-2q</math>.  
# <math>q_1=q,\quad q_2=-2q</math>.  
# <math>q_1</math> y <math>q_2</math> arbitrarios.
# <math>q_1</math> y <math>q_2</math> arbitrarios.
 +
 +
[[Categoría:Problemas de campo eléctrico F2 GIA]]
== Solución ==
== Solución ==
Línea 14: Línea 16:
\left\{
\left\{
\begin{array}{ll}
\begin{array}{ll}
-
\dfrac{q}{4\,\pi\,\varepsilon_0}\,\dfrac{1}{(x_P-x_1)^2}\,\vec{\imath} & x_P>x_1 \\
 
-
& \\
 
-\dfrac{q}{4\,\pi\,\varepsilon_0}\,\dfrac{1}{(x_P-x_1)^2}\,\vec{\imath} & x_P<x_1 \\
-\dfrac{q}{4\,\pi\,\varepsilon_0}\,\dfrac{1}{(x_P-x_1)^2}\,\vec{\imath} & x_P<x_1 \\
 +
& \\
 +
\dfrac{q}{4\,\pi\,\varepsilon_0}\,\dfrac{1}{(x_P-x_1)^2}\,\vec{\imath} & x_P>x_1 \\
\end{array}
\end{array}
\right.
\right.
Línea 29: Línea 31:
\left\{
\left\{
\begin{array}{ll}
\begin{array}{ll}
-
\dfrac{q}{4\,\pi\,\varepsilon_0}\,\dfrac{1}{x_P^2}\,\vec{\imath} & x_P>0 \\
+
-\dfrac{q_1}{4\,\pi\,\varepsilon_0}\,\dfrac{1}{x_P^2}\,\vec{\imath} & x_P<0 \\
& \\
& \\
-
-\dfrac{q}{4\,\pi\,\varepsilon_0}\,\dfrac{1}{x_P^2}\,\vec{\imath} & x_P<0 \\
+
\dfrac{q_1}{4\,\pi\,\varepsilon_0}\,\dfrac{1}{x_P^2}\,\vec{\imath} & x_P>0 \\
\end{array}
\end{array}
\right.
\right.
Línea 42: Línea 44:
\left\{
\left\{
\begin{array}{ll}
\begin{array}{ll}
-
\dfrac{q}{4\,\pi\,\varepsilon_0}\,\dfrac{1}{(x_P-x_2)^2}\,\vec{\imath} & x_P>x_2 \\
+
-\dfrac{q_2}{4\,\pi\,\varepsilon_0}\,\dfrac{1}{(x_P-x_2)^2}\,\vec{\imath} & x_P<x_2 \\
& \\
& \\
-
-\dfrac{q}{4\,\pi\,\varepsilon_0}\,\dfrac{1}{(x_P-x_2)^2}\,\vec{\imath} & x_P<x_2 \\
+
\dfrac{q_2}{4\,\pi\,\varepsilon_0}\,\dfrac{1}{(x_P-x_2)^2}\,\vec{\imath} & x_P>x_2 \\
\end{array}
\end{array}
\right.
\right.
Línea 50: Línea 52:
</center>
</center>
Hay que distinguir tres zonas en el eje eje, a la izquierda de <math>q_1 </math>, entre las dos cargas y a la derecha de <math>q_2 </math>. Estas tres zonas vienen dadas por <math>(x_P<0) </math>, <math>0<x_P<x_2 </math> y <math>x_P>x_2 </math>, respectivamente.
Hay que distinguir tres zonas en el eje eje, a la izquierda de <math>q_1 </math>, entre las dos cargas y a la derecha de <math>q_2 </math>. Estas tres zonas vienen dadas por <math>(x_P<0) </math>, <math>0<x_P<x_2 </math> y <math>x_P>x_2 </math>, respectivamente.
 +
 +
La forma final del campo es
 +
<center>
 +
<math>
 +
\vec{E}(x)
 +
=
 +
\left\{
 +
\begin{array}{ll}
 +
-\dfrac{1}{4\,\pi\,\varepsilon_0}
 +
\left(
 +
\dfrac{q_1}{x_P^2} + \dfrac{q_2}{|x_P-x_2|^2}
 +
\right)
 +
& x_P<0
 +
\\ & \\
 +
\dfrac{1}{4\,\pi\,\varepsilon_0}
 +
\left(
 +
\dfrac{q_1}{x_P^2} - \dfrac{q_2}{|x_P-x_2|^2}
 +
\right)
 +
& 0<x_P<x_2
 +
\\ & \\
 +
\dfrac{1}{4\,\pi\,\varepsilon_0}
 +
\left(
 +
\dfrac{q_1}{x_P^2} + \dfrac{q_2}{|x_P-x_2|^2}
 +
\right)
 +
& x_P >x_2
 +
\end{array}
 +
\right.
 +
</math>
 +
</center>
 +
 +
Examinamos ahora los tres casos particulares
 +
 +
=== Cargas iguales en magnitud y signo===
 +
Tenemos
 +
<center>
 +
<math>
 +
q_1=q\qquad x_1=0\qquad\qquad\qquad q_2=q\qquad x_2 = d
 +
</math>
 +
</center>
 +
El campo en la línea que las une es
 +
<center>
 +
<math>
 +
\vec{E}(x)
 +
=
 +
\left\{
 +
\begin{array}{ll}
 +
-\dfrac{q}{4\,\pi\,\varepsilon_0}
 +
\left(
 +
\dfrac{1}{x_P^2} + \dfrac{1}{(x_P-d)^2}
 +
\right)
 +
& x_P<0
 +
\\ & \\
 +
\dfrac{q}{4\,\pi\,\varepsilon_0}
 +
\left(
 +
\dfrac{1}{x_P^2} - \dfrac{1}{(x_P-d)^2}
 +
\right)
 +
& 0<x_P<d
 +
\\ & \\
 +
\dfrac{q}{4\,\pi\,\varepsilon_0}
 +
\left(
 +
\dfrac{1}{x_P^2} + \dfrac{1}{(x_P-d)^2}
 +
\right)
 +
& x_P >d
 +
\end{array}
 +
\right.
 +
</math>
 +
</center>
 +
La única región en la que se puede anular el campo es entre las dos cargas. Para encontrar el valor de <math>x_P </math> anulamos la expresión del campo
 +
<center>
 +
<math>
 +
\dfrac{1}{x_P^2} - \dfrac{1}{(x_P-d)^2}=0 \Longrightarrow x_P=d/2
 +
</math>
 +
</center>
 +
El campo se anula en el punto medio entre las cargas.
 +
 +
=== Cargas iguales en magnitud y signo contrario===
 +
Tenemos
 +
<center>
 +
<math>
 +
q_1=q\qquad x_1=0\qquad\qquad\qquad q_2=-q\qquad x_2 = d
 +
</math>
 +
</center>
 +
El campo en la línea que las une es
 +
<center>
 +
<math>
 +
\vec{E}(x)
 +
=
 +
\left\{
 +
\begin{array}{ll}
 +
-\dfrac{q}{4\,\pi\,\varepsilon_0}
 +
\left(
 +
\dfrac{1}{x_P^2} - \dfrac{1}{(x_P-d)^2}
 +
\right)
 +
& x_P<0
 +
\\ & \\
 +
\dfrac{q}{4\,\pi\,\varepsilon_0}
 +
\left(
 +
\dfrac{1}{x_P^2} + \dfrac{1}{(x_P-d)^2}
 +
\right)
 +
& 0<x_P<d
 +
\\ & \\
 +
\dfrac{q}{4\,\pi\,\varepsilon_0}
 +
\left(
 +
\dfrac{1}{x_P^2} - \dfrac{1}{(x_P-d)^2}
 +
\right)
 +
& x_P >d
 +
\end{array}
 +
\right.
 +
</math>
 +
</center>
 +
En este caso el campo podría anulares a la izquierda y la derecha de las cargas. Fijémonos en el lado izquierdo.
 +
Para encontrar el valor de <math>x_P </math> anulamos la expresión del campo
 +
<center>
 +
<math>
 +
\dfrac{1}{x_P^2} - \dfrac{1}{(x_P-d)^2}=0 \Longrightarrow x_P=d/2
 +
</math>
 +
</center>
 +
Este punto corresponde a la región entre cargas. Pero estamos considerando valores negativos de <math>x_P </math>. Como este punto está fuera de este rango, esto quiere decir que el campo no se anula a la izquierda de las cargas.
 +
 +
El mismo razonamiento vale para la región a la derecha. La conclusión es que '''el campo no se anula en ningún punto de la línea que une las cargas'''. En las regiones en las que el sentido de los campos es distinto, las magnitudes son siempre diferentes, pues al ser igual el valor absoluto de las cargas, la que esté más próxima produce un campo más intenso.
 +
 +
 +
 +
=== Cargas  distintas en magnitud y signo ===
 +
Tenemos
 +
<center>
 +
<math>
 +
q_1=q\qquad x_1=0\qquad\qquad\qquad q_2=-2q\qquad x_2 = d
 +
</math>
 +
</center>
 +
El campo en la línea que las une es
 +
<center>
 +
<math>
 +
\vec{E}(x)
 +
=
 +
\left\{
 +
\begin{array}{ll}
 +
-\dfrac{q}{4\,\pi\,\varepsilon_0}
 +
\left(
 +
\dfrac{1}{x_P^2} - \dfrac{2}{(x_P-d)^2}
 +
\right)
 +
& x_P<0
 +
\\ & \\
 +
\dfrac{q}{4\,\pi\,\varepsilon_0}
 +
\left(
 +
\dfrac{1}{x_P^2} + \dfrac{2}{(x_P-d)^2}
 +
\right)
 +
& 0<x_P<d
 +
\\ & \\
 +
\dfrac{q}{4\,\pi\,\varepsilon_0}
 +
\left(
 +
\dfrac{1}{x_P^2} - \dfrac{2}{(x_P-d)^2}
 +
\right)
 +
& x_P >d
 +
\end{array}
 +
\right.
 +
</math>
 +
</center>
 +
La única región en la que se puede anular el campo es entre las dos cargas. Para encontrar el valor de <math>x_P </math> anulamos la expresión del campo
 +
<center>
 +
<math>
 +
\dfrac{1}{x_P^2} - \dfrac{1}{(x_P-d)^2}=0 \Longrightarrow x_P=d/2
 +
</math>
 +
</center>
 +
El campo no se puede anular entre las cargas.
 +
 +
La ecuación para encontrar el punto en el que se anula el campo es la misma a la izquierda y a la derecha de las cargas. Para ello debe ocurrir
 +
<center>
 +
<math>
 +
\dfrac{1}{x_P^2} - \dfrac{2}{(x_P-d)^2} = 0
 +
\Rightarrow
 +
x_P^2 + 2\,d\,x_p - d^2=0
 +
\Rightarrow
 +
x_P =
 +
\left\{
 +
\begin{array}{l}
 +
x_P = 0.41\,d \\ x_P=-2.41\,d
 +
\end{array}
 +
\right.
 +
</math>
 +
</center>
 +
La primera solución es un punto entre las cargas, con lo cual no puede ocurrir. El punto donde se anula el campo es el segundo, es decir, a la izquierda de las cargas. En esta zona los campos de las dos cargas tienen sentidos opuestos. Como la carga negativa es mayor en valor absoluto hay un punto donde la intensidad de los dos campos puede igualarse. Esto no ocurre a la derecha de las cargas. En esta zona la magnitud del campo de la carga negativa es siempre mayor que el de la positiva.

última version al 00:52 10 mar 2012

Contenido

1 Enunciado

Se tienen dos cargas puntuales q1 y q2 separadas por una distancia d. Determina el punto sobre la línea que las une en el que el campo eléctrico se anula para cada uno de estos casos

  1. q_1=q,\quad q_2=q.
  2. q_1=q,\quad q_2=-q.
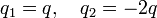  3. q_1=q,\quad q_2=-2q.
  4. q1 y q2 arbitrarios.

2 Solución

Vamos a hacer el caso general con valores arbitrarios de las cargas. Consideramos una carga q situada en una posición arbitraria del eje OX dada por la coordenada x1. El campo que produce en un punto Pcualquiera de ese eje es

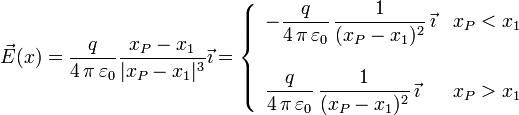
\vec{E}(x) = \dfrac{q}{4\,\pi\,\varepsilon_0}\dfrac{x_P-x_1}{|x_P-x_1|^3}\vec{\imath} = \left\{ \begin{array}{ll} -\dfrac{q}{4\,\pi\,\varepsilon_0}\,\dfrac{1}{(x_P-x_1)^2}\,\vec{\imath} & x_P<x_1 \\ & \\ \dfrac{q}{4\,\pi\,\varepsilon_0}\,\dfrac{1}{(x_P-x_1)^2}\,\vec{\imath} & x_P>x_1 \\ \end{array} \right.

Si q > 0 el campo apunta hacia la derecha a la derecha de la carga (xP > x1) y hacia la izquierda a la izquierda de la carga (xP < x1).

Si tenemos dos cargas, q1 y q2 situadas en los puntos del eje OX de coordenadas respectivas x1 y x2 respectivamente, el campo total en un punto P arbitrario del eje es la suma de los campos de las dos cargas. Para simplificar, vamos a situar el origen en la posición de la carga q1, (x1 = 0) y que la otra carga está a su derecha (x2 > 0). El campo de cada carga es

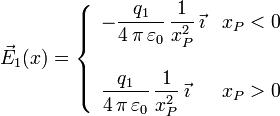
\vec{E}_1(x) = \left\{ \begin{array}{ll} -\dfrac{q_1}{4\,\pi\,\varepsilon_0}\,\dfrac{1}{x_P^2}\,\vec{\imath} & x_P<0 \\ & \\ \dfrac{q_1}{4\,\pi\,\varepsilon_0}\,\dfrac{1}{x_P^2}\,\vec{\imath} & x_P>0 \\ \end{array} \right.

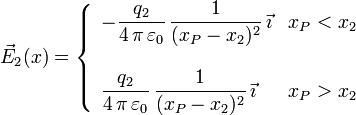
\vec{E}_2(x) = \left\{ \begin{array}{ll} -\dfrac{q_2}{4\,\pi\,\varepsilon_0}\,\dfrac{1}{(x_P-x_2)^2}\,\vec{\imath} & x_P<x_2 \\ & \\ \dfrac{q_2}{4\,\pi\,\varepsilon_0}\,\dfrac{1}{(x_P-x_2)^2}\,\vec{\imath} & x_P>x_2 \\ \end{array} \right.

Hay que distinguir tres zonas en el eje eje, a la izquierda de q1, entre las dos cargas y a la derecha de q2. Estas tres zonas vienen dadas por (xP < 0), 0 < xP < x2 y xP > x2, respectivamente.

La forma final del campo es

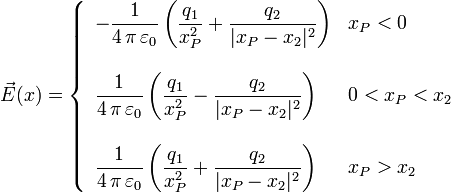
\vec{E}(x) = \left\{ \begin{array}{ll} -\dfrac{1}{4\,\pi\,\varepsilon_0} \left( \dfrac{q_1}{x_P^2} + \dfrac{q_2}{|x_P-x_2|^2} \right) & x_P<0 \\ & \\ \dfrac{1}{4\,\pi\,\varepsilon_0} \left( \dfrac{q_1}{x_P^2} - \dfrac{q_2}{|x_P-x_2|^2} \right) & 0<x_P<x_2 \\ & \\ \dfrac{1}{4\,\pi\,\varepsilon_0} \left( \dfrac{q_1}{x_P^2} + \dfrac{q_2}{|x_P-x_2|^2} \right) & x_P >x_2 \end{array} \right.

Examinamos ahora los tres casos particulares

2.1 Cargas iguales en magnitud y signo

Tenemos

q_1=q\qquad x_1=0\qquad\qquad\qquad q_2=q\qquad x_2 = d

El campo en la línea que las une es

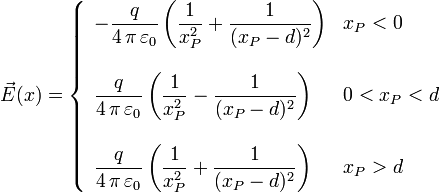
\vec{E}(x) = \left\{ \begin{array}{ll} -\dfrac{q}{4\,\pi\,\varepsilon_0} \left( \dfrac{1}{x_P^2} + \dfrac{1}{(x_P-d)^2} \right) & x_P<0 \\ & \\ \dfrac{q}{4\,\pi\,\varepsilon_0} \left( \dfrac{1}{x_P^2} - \dfrac{1}{(x_P-d)^2} \right) & 0<x_P<d \\ & \\ \dfrac{q}{4\,\pi\,\varepsilon_0} \left( \dfrac{1}{x_P^2} + \dfrac{1}{(x_P-d)^2} \right) & x_P >d \end{array} \right.

La única región en la que se puede anular el campo es entre las dos cargas. Para encontrar el valor de xP anulamos la expresión del campo

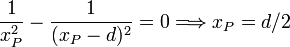
\dfrac{1}{x_P^2} - \dfrac{1}{(x_P-d)^2}=0 \Longrightarrow x_P=d/2

El campo se anula en el punto medio entre las cargas.

2.2 Cargas iguales en magnitud y signo contrario

Tenemos

q_1=q\qquad x_1=0\qquad\qquad\qquad q_2=-q\qquad x_2 = d

El campo en la línea que las une es

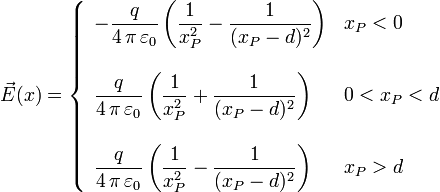
\vec{E}(x) = \left\{ \begin{array}{ll} -\dfrac{q}{4\,\pi\,\varepsilon_0} \left( \dfrac{1}{x_P^2} - \dfrac{1}{(x_P-d)^2} \right) & x_P<0 \\ & \\ \dfrac{q}{4\,\pi\,\varepsilon_0} \left( \dfrac{1}{x_P^2} + \dfrac{1}{(x_P-d)^2} \right) & 0<x_P<d \\ & \\ \dfrac{q}{4\,\pi\,\varepsilon_0} \left( \dfrac{1}{x_P^2} - \dfrac{1}{(x_P-d)^2} \right) & x_P >d \end{array} \right.

En este caso el campo podría anulares a la izquierda y la derecha de las cargas. Fijémonos en el lado izquierdo. Para encontrar el valor de xP anulamos la expresión del campo

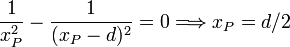
\dfrac{1}{x_P^2} - \dfrac{1}{(x_P-d)^2}=0 \Longrightarrow x_P=d/2

Este punto corresponde a la región entre cargas. Pero estamos considerando valores negativos de xP. Como este punto está fuera de este rango, esto quiere decir que el campo no se anula a la izquierda de las cargas.

El mismo razonamiento vale para la región a la derecha. La conclusión es que el campo no se anula en ningún punto de la línea que une las cargas. En las regiones en las que el sentido de los campos es distinto, las magnitudes son siempre diferentes, pues al ser igual el valor absoluto de las cargas, la que esté más próxima produce un campo más intenso.


2.3 Cargas distintas en magnitud y signo

Tenemos

q_1=q\qquad x_1=0\qquad\qquad\qquad q_2=-2q\qquad x_2 = d

El campo en la línea que las une es

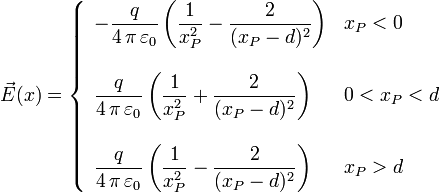
\vec{E}(x) = \left\{ \begin{array}{ll} -\dfrac{q}{4\,\pi\,\varepsilon_0} \left( \dfrac{1}{x_P^2} - \dfrac{2}{(x_P-d)^2} \right) & x_P<0 \\ & \\ \dfrac{q}{4\,\pi\,\varepsilon_0} \left( \dfrac{1}{x_P^2} + \dfrac{2}{(x_P-d)^2} \right) & 0<x_P<d \\ & \\ \dfrac{q}{4\,\pi\,\varepsilon_0} \left( \dfrac{1}{x_P^2} - \dfrac{2}{(x_P-d)^2} \right) & x_P >d \end{array} \right.

La única región en la que se puede anular el campo es entre las dos cargas. Para encontrar el valor de xP anulamos la expresión del campo

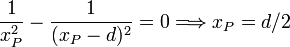
\dfrac{1}{x_P^2} - \dfrac{1}{(x_P-d)^2}=0 \Longrightarrow x_P=d/2

El campo no se puede anular entre las cargas.

La ecuación para encontrar el punto en el que se anula el campo es la misma a la izquierda y a la derecha de las cargas. Para ello debe ocurrir

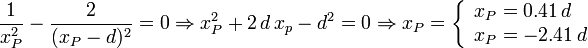
\dfrac{1}{x_P^2} - \dfrac{2}{(x_P-d)^2} = 0 \Rightarrow x_P^2 + 2\,d\,x_p - d^2=0 \Rightarrow x_P = \left\{ \begin{array}{l} x_P = 0.41\,d \\ x_P=-2.41\,d \end{array} \right.

La primera solución es un punto entre las cargas, con lo cual no puede ocurrir. El punto donde se anula el campo es el segundo, es decir, a la izquierda de las cargas. En esta zona los campos de las dos cargas tienen sentidos opuestos. Como la carga negativa es mayor en valor absoluto hay un punto donde la intensidad de los dos campos puede igualarse. Esto no ocurre a la derecha de las cargas. En esta zona la magnitud del campo de la carga negativa es siempre mayor que el de la positiva.

Obtenido de "http://tesla.us.es/wiki/index.php/Campo_el%C3%A9ctrico_entre_dos_cargas_puntuales_GIA"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 00:52, 10 mar 2012. - Esta página ha sido visitada 21.526 veces. - Aviso legal - Acerca de Laplace