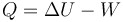Entrar Página Discusión Historial Go to the site toolbox

Sucesión de tres procesos cuasiestáticos

De Laplace

(Diferencias entre revisiones)
Línea 99: Línea 99:
El signo del trabajo nos dice que en realidad es el gas el que realiza el trabajo sobre el ambiente.
El signo del trabajo nos dice que en realidad es el gas el que realiza el trabajo sobre el ambiente.
==Energía y calor==
==Energía y calor==
 +
La energía interna de un gas ideal depende solamente de su temperatura
 +
 +
<center><math>U = U_0 + n c_v T\,</math></center>
 +
 +
siendo la capacidad calorífica molar para el aire aproximadamente igual a la de un gas diatómico
 +
 +
<center><math>c_v = \frac{5}{2}R = 20.8\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{mol}}</math></center>
 +
 +
La variación de la energía interna en cualquier proceso es proporcional a la diferencia de temperaturas
 +
 +
<center><math>\Delta U = nc_v\,\Delta T</math></center>
 +
 +
independientemente de si el proceso es a presión constante, a volumen constante o como sea, por tratarse de una función de estado.
 +
 +
Una vez que calculemos la variación en la energía, podemos hallar el calor que entra en el gas por el primer principio de la termodinámica
 +
 +
<center><math>Q = \Delta U - W\,</math></center>
[[Categoría:Problemas del primer principio de la termodinámica (GIE)]]
[[Categoría:Problemas del primer principio de la termodinámica (GIE)]]

Revisión de 18:57 1 mar 2012

Contenido

1 Enunciado

Un cilindro de 20 cm de diámetro contiene aire y está cerrado por un émbolo. Inicialmente el aire tiene una temperatura de 27 °C y una presión de 100 kPa, que también es la presión exterior, estando el émbolo a 10 cm del fondo. Entonces se realiza el siguiente proceso cuasiestático

I: Se atornilla el émbolo y se calienta el aire hasta 327 °C, sumergiéndolo en un baño a esta temperatura.
II: Se libera el émbolo lentamente, dejando que se expanda el aire hasta que su presión vuelve a ser la inicial. En este proceso el aire se mantiene a la temperatura de 327 °C.
III: Con el émbolo libre, se enfría gradualmente hasta que la temperatura vuelve a ser la inicial.

Para este proceso:

  1. Halle la presión, volumen y temperatura al final de cada fase del proceso.
  2. Calcule el trabajo en cada fase, así como el trabajo neto total.
  3. Calcule la variación en la energía interna y el calor en cada paso y su variación neta.

2 Presión, volumen y temperatura

2.1 Estado inicial

Inicialmente tenemos que la presión y la temperatura valen

p_A=100\,\mathrm{kPa}\qquad\qquad T_A=(273+27)\mathrm{K}=300\,\mathrm{K}

mientras que el volumen es el de un cilindro

V_A = \pi r^2 h = \pi(0.1\,\mathrm{m})^2(0.1\mathrm{m}) = 0.00314\,\mathrm{m}^3 = 3.14\,\mathrm{dm}^3

2.2 Tras el primer paso

El primer paso ocurre a volumen constante, por estar el pistón atornillado, con lo que el voluemn final es el mismo que el inicial

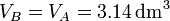
V_B = V_A = 3.14\,\mathrm{dm}^3

La temperatura ha aumentado en 300°C

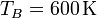
T_B = 600\,\mathrm{K}

y la presión aumenta en la misma proporción que la temperatura

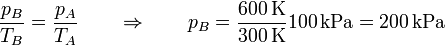
\frac{p_B}{T_B}=\frac{p_A}{T_A}\qquad\Rightarrow\qquad p_B = \frac{600\,\mathrm{K}}{300\,\mathrm{K}}100\,\mathrm{kPa} = 200\,\mathrm{kPa}

2.3 Tras el segundo paso

En el segundo paso tenemos una expansión isoterma, siendo la temperatura final igual a la que había al final del paso anterior

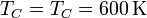
T_C = T_C = 600\,\mathrm{K}

mientras que la presión final vuelve a ser la que había al principio

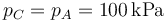
p_C = p_A = 100\,\mathrm{kPa}

El volumen final lo podemos obtener particularizando la ley d elos gases ideales para temperatura constante, es decir, aplicando la ley de Boyle

p_CV_C=p_BV_B\qquad\Rightarrow\qquad V_C = \frac{200\,\mathrm{kPa}}{100\,\mathrm{kPa}}3.14\,\mathrm{dm}^3 = 6.28\,\mathrm{dm}^3

2.4 Estado final

Por último, dejando el émbolo libre, la temperatura vuelve a ser la inicial, manteniéndose constante la presión

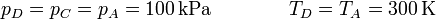
p_D = p_C=p_A = 100\,\mathrm{kPa}\qquad\qquad T_D = T_A = 300\,\mathrm{K}

La ley de los gases ideales se reduce en este caso a la ley de Charles

\frac{V_D}{T_D}=\frac{V_C}{T_C} \qquad\Rightarrow\qquad V_D = \frac{300\,\mathrm{K}}{600\,\mathrm{K}}6.28\,\mathrm{dm}^3 = 3.14\,\mathrm{dm}^3

Al ser la presión y la temperatura finales iguales a las de partida también lo es el volumen. El estado D es el mismo que el estado A y el proceso es por tanto un ciclo.

2.5 Representación gráfica

Gráficamente este proceso se compone de tres tramos:

  • Un calentamiento a volumen constante, que corresponde a una recta vertical.
  • Una expansión isoterma, que se representa por un arco de hipérbola.
  • Una compresión a presión constante, que en la gráfica queda como una recta horizontal.

3 Trabajo

Podemos hallar el trabajo sobre el gas en cada paso a partir de la evolución de sus variables de estado, si suponemos que todos los procesos son cuasiestáticos.

3.1 Calentamiento a volumen constante

Al permanecer constante el volumen, no se realiza trabajo sobre el gas

W_{A\to B} = 0\,

3.2 Expansión isoterma

Cuando la temperatura permanece constante, podemos calcular el trabajo con ayuda de la ecuación de estado de la ley de Boyle. En cualquier punto del camino

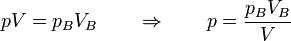
pV = p_BV_B\qquad\Rightarrow\qquad p = \frac{p_BV_B}{V}

lo que nos da el trabajo

W_{B\to C}=-\int_B^C p\,\mathrm{d}V = -p_BV_B\int_{V_B}^{V_C}\frac{\mathrm{d}V}{V}=-p_BV_B\ln\left(\frac{V_C}{V_B}\right)

En nuestro caso

W_{B\to C} = -(2\times 10^5\mathrm{Pa})(0.00314\,\mathrm{m}^3)(2) = -435\,\mathrm{J}

3.3 Compresión isóbara

En el tercer paso, el volumen se reduce a presión constante, lo que da un trabajo equivalente gráficamente al área de un rectángulo

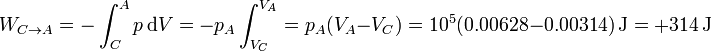
W_{C\to A} = -\int_C^A p\,\mathrm{d} V = -p_A\int_{V_C}^{V_A} = p_A(V_A-V_C) = 10^5(0.00628 - 0.00314)\,\mathrm{J} = +314\,\mathrm{J}

3.4 Trabajo neto

El trabajo neto sobre el gas en el ciclo será la suma de los trabajos individuales

W = -\oint p\,\mathrm{d}V = W_{A\to B}+W_{B\to C}+W_{C\to A}=\left(0 -435+314\right)\mathrm{J}= -121\,\mathrm{J}

El signo del trabajo nos dice que en realidad es el gas el que realiza el trabajo sobre el ambiente.

4 Energía y calor

La energía interna de un gas ideal depende solamente de su temperatura

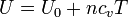
U = U_0 + n c_v T\,

siendo la capacidad calorífica molar para el aire aproximadamente igual a la de un gas diatómico

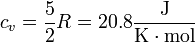
c_v = \frac{5}{2}R = 20.8\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{mol}}

La variación de la energía interna en cualquier proceso es proporcional a la diferencia de temperaturas

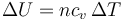
\Delta U = nc_v\,\Delta T

independientemente de si el proceso es a presión constante, a volumen constante o como sea, por tratarse de una función de estado.

Una vez que calculemos la variación en la energía, podemos hallar el calor que entra en el gas por el primer principio de la termodinámica

Q = \Delta U - W\,
Obtenido de "http://tesla.us.es/wiki/index.php/Sucesi%C3%B3n_de_tres_procesos_cuasiest%C3%A1ticos"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace