Sucesión de tres procesos cuasiestáticos
De Laplace
| Línea 22: | Línea 22: | ||
<center><math>V_0 = \pi r^2 h = \pi(0.1\,\mathrm{m})^2(0.1\mathrm{m}) = 0.00314\,\mathrm{m}^3 = 3.14\,\mathrm{l}</math></center> | <center><math>V_0 = \pi r^2 h = \pi(0.1\,\mathrm{m})^2(0.1\mathrm{m}) = 0.00314\,\mathrm{m}^3 = 3.14\,\mathrm{l}</math></center> | ||
| - | ===Tras el paso | + | ===Tras el primer paso=== |
El primer paso ocurre a volumen constante, por estar el pistón atornillado, con lo que el voluemn final es el mismo que el inicial | El primer paso ocurre a volumen constante, por estar el pistón atornillado, con lo que el voluemn final es el mismo que el inicial | ||
| Línea 35: | Línea 35: | ||
<center><math>\frac{p_1}{T_1}=\frac{p_0}{T_0}\qquad\Rightarrow\qquad p_1 = \frac{600\,\mathrm{K}}{300\,\mathrm{K}}100\,\mathrm{kPa} = 200\,\mathrm{kPa}</math></center> | <center><math>\frac{p_1}{T_1}=\frac{p_0}{T_0}\qquad\Rightarrow\qquad p_1 = \frac{600\,\mathrm{K}}{300\,\mathrm{K}}100\,\mathrm{kPa} = 200\,\mathrm{kPa}</math></center> | ||
| - | ===Tras el paso | + | ===Tras el segundo paso=== |
| + | En el segundo paso tenemos una expansión isoterma, siendo la temperatura final igual a la que había al final del paso anterior | ||
| + | |||
| + | <center><math>T_2 = T_1 = 600\,\mathrm{K}</math></center> | ||
| + | |||
| + | mientras que la presión final vuelve a ser la que había al principio | ||
| + | |||
| + | <center><math>p_2 = p_0 = 100\,\mathrm{kPa}</math></center> | ||
| + | |||
| + | El volumen final lo podemos obtener particularizando la ley d elos gases ideales para temperatura constante, es decir, aplicando la ley de Boyle | ||
| + | |||
| + | <center><math>p_2V_2=p_1V_1\qquad\Rightarrow\qquad V_2 = \frac{200\,\mathrm{kPa}}{100\,\mathrm{kPa}}0.00314\,\mathrm{m}^3 = 0.00628\,\mathrm{m}^3</math></center> | ||
| + | |||
===Estado final=== | ===Estado final=== | ||
| + | Por último, dejando el émbolo libre, la temperatura vuelve a ser la inicial, manteniéndose constante la presión | ||
| + | |||
| + | <center><math>p_3 = p_2=p_0 = 100\,\mathrm{kPa}\qquad\qquad T_3 = T_0 = 300\,\mathrm{K}</math></center> | ||
| + | |||
| + | La ley de los gases ideales se reduce en este caso a la ley de Charles | ||
| + | |||
| + | <center><math>\frac{V_3}{T_3}=\frac{V_2}{T_2} \qquad\Rightarrow\qquad V_3 = \frac{300\,\mathrm{K}}{600\,\mathrm{K}}0.00628\,\mathrm{m}^3 = 0.00314\,\mathrm{m}^3</math></center> | ||
| + | |||
| + | Al ser la presión y la temperatura finales iguales a las de partida también lo es el volumen y el proceso es por tanto un ciclo. | ||
| + | |||
| + | ===Representación gráfica=== | ||
| + | Gráficamente este proceso se compone de tres tramos: | ||
| + | |||
| + | * Un calentamiento a volumen constante, que corresponde a una recta vertical. | ||
| + | * Una expansión isoterma, que se representa por un arco de hipérbola. | ||
| + | * Una compresión a presión constante, que en la gráfica queda como una recta horizontal. | ||
| + | |||
| + | |||
==Trabajo== | ==Trabajo== | ||
==Energía y calor== | ==Energía y calor== | ||
[[Categoría:Problemas del primer principio de la termodinámica (GIE)]] | [[Categoría:Problemas del primer principio de la termodinámica (GIE)]] | ||
Revisión de 18:13 1 mar 2012
Contenido |
1 Enunciado
Un cilindro de 20 cm de diámetro contiene aire y está cerrado por un émbolo. Inicialmente el aire tiene una temperatura de 27 °C y una presión de 100 kPa, que también es la presión exterior, estando el émbolo a 10 cm del fondo. Entonces se realiza el siguiente proceso cuasiestático
- I: Se atornilla el émbolo y se calienta el aire hasta 327 °C, sumergiéndolo en un baño a esta temperatura.
- II: Se libera el émbolo lentamente, dejando que se expanda el aire hasta que su presión vuelve a ser la inicial. En este proceso el aire se mantiene a la temperatura de 327 °C.
- III: Con el émbolo libre, se enfría gradualmente hasta que la temperatura vuelve a ser la inicial.
Para este proceso:
- Halle la presión, volumen y temperatura al final de cada fase del proceso.
- Calcule el trabajo en cada fase, así como el trabajo neto total.
- Calcule la variación en la energía interna y el calor en cada paso y su variación neta.
2 Presión, volumen y temperatura
2.1 Estado inicial
Inicialmente tenemos que la presión y la temperatura valen

mientras que el volumen es el de un cilindro

2.2 Tras el primer paso
El primer paso ocurre a volumen constante, por estar el pistón atornillado, con lo que el voluemn final es el mismo que el inicial

La temperatura ha aumentado en 300°C
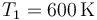
y la presión aumenta en la misma proporción que la temperatura

2.3 Tras el segundo paso
En el segundo paso tenemos una expansión isoterma, siendo la temperatura final igual a la que había al final del paso anterior
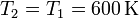
mientras que la presión final vuelve a ser la que había al principio
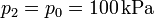
El volumen final lo podemos obtener particularizando la ley d elos gases ideales para temperatura constante, es decir, aplicando la ley de Boyle
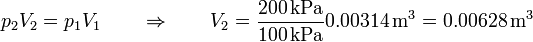
2.4 Estado final
Por último, dejando el émbolo libre, la temperatura vuelve a ser la inicial, manteniéndose constante la presión
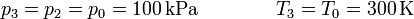
La ley de los gases ideales se reduce en este caso a la ley de Charles
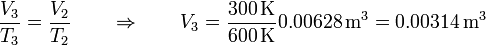
Al ser la presión y la temperatura finales iguales a las de partida también lo es el volumen y el proceso es por tanto un ciclo.
2.5 Representación gráfica
Gráficamente este proceso se compone de tres tramos:
- Un calentamiento a volumen constante, que corresponde a una recta vertical.
- Una expansión isoterma, que se representa por un arco de hipérbola.
- Una compresión a presión constante, que en la gráfica queda como una recta horizontal.





