Variación de la presión de los neumáticos
De Laplace
(Página creada con '==Enunciado== Un automovilista llena los neumáticos de su coche a una presión manométrica de 2.4 bar un día de enero en que la tempera exterior es de 5°C. Si no l…') |
|||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
Un automovilista llena los neumáticos de su coche a una presión manométrica de 2.4 bar un día de enero en que la tempera exterior es de 5°C. Si no los toca en seis meses y no hay fugas, ¿cuál será la presión manométrica un día de julio a 40°C? ¿Qué proporción de aire debe extraer de cada neumático para devolver la presión a 2.4 bar? Si tras reducir la presión se despreocupa otros seis meses, ¿cuál será la presión manométrica cuando vuelva a hacer 5°C? Desprecie la dilatación de los neumáticos. | Un automovilista llena los neumáticos de su coche a una presión manométrica de 2.4 bar un día de enero en que la tempera exterior es de 5°C. Si no los toca en seis meses y no hay fugas, ¿cuál será la presión manométrica un día de julio a 40°C? ¿Qué proporción de aire debe extraer de cada neumático para devolver la presión a 2.4 bar? Si tras reducir la presión se despreocupa otros seis meses, ¿cuál será la presión manométrica cuando vuelva a hacer 5°C? Desprecie la dilatación de los neumáticos. | ||
| - | |||
==Solución== | ==Solución== | ||
| + | Si despreciamos la dilatación de los neumáticos se trata de un proceso de calentamiento a volumen constante, para el cual se cumple | ||
| + | |||
| + | <center><math>V_1=V_2 \qquad\Rightarrow\qquad \frac{p_1}{T_1}=\frac{p_2}{T_2}</math></center> | ||
| + | |||
| + | En el estado inicial la temperatura 5°C y la presión manométrica es de 2.4 bares. La presión absoluta será ésta, más la atmosférica, que es aproximadamente 1 bar (una atmósfera estándar son en realidad 1,013 bares, pero teniendo en cuenta que se nos da la presión manométrica con solo dos cifras significativas, no hace falta introducir más decimales). | ||
| + | |||
| + | <center><math>p_1 \simeq 3.4\,\mathrm{bar}\qquad \qquad T_1 = 278\,\mathrm{K}</math></center> | ||
| + | |||
| + | En el estado final, en verano, la temperatura a aumentado | ||
| + | |||
| + | <center><math>T_2 = 313\,\mathrm{K}</math></center> | ||
| + | |||
| + | Esto nos da la presión absoluta en verano | ||
| + | |||
| + | <center><math>p_2 = \frac{T_2}{T_1}p_1 = \frac{313}{278}3.4\,\mathrm{bar} = 3.8\,\mathrm{bar} | ||
| + | </math></center> | ||
| + | |||
| + | y la manométrica | ||
| + | |||
| + | <center><math>\Delta p_2 = (3.8-1.0)\,\mathrm{bar}=2.8\,\mathrm{bar}</math></center> | ||
| + | |||
[[Categoría:Problemas de introducción a la termodinámica (GIE)]] | [[Categoría:Problemas de introducción a la termodinámica (GIE)]] | ||
Revisión de 00:01 16 feb 2012
1 Enunciado
Un automovilista llena los neumáticos de su coche a una presión manométrica de 2.4 bar un día de enero en que la tempera exterior es de 5°C. Si no los toca en seis meses y no hay fugas, ¿cuál será la presión manométrica un día de julio a 40°C? ¿Qué proporción de aire debe extraer de cada neumático para devolver la presión a 2.4 bar? Si tras reducir la presión se despreocupa otros seis meses, ¿cuál será la presión manométrica cuando vuelva a hacer 5°C? Desprecie la dilatación de los neumáticos.
2 Solución
Si despreciamos la dilatación de los neumáticos se trata de un proceso de calentamiento a volumen constante, para el cual se cumple
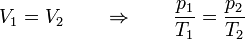
En el estado inicial la temperatura 5°C y la presión manométrica es de 2.4 bares. La presión absoluta será ésta, más la atmosférica, que es aproximadamente 1 bar (una atmósfera estándar son en realidad 1,013 bares, pero teniendo en cuenta que se nos da la presión manométrica con solo dos cifras significativas, no hace falta introducir más decimales).

En el estado final, en verano, la temperatura a aumentado
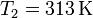
Esto nos da la presión absoluta en verano
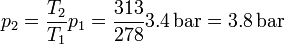
y la manométrica