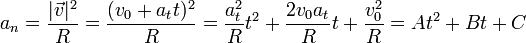Movimiento con aceleración tangencial constante
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Una partícula se mueve a lo largo de una circunferencia de radio <math>R</math> en el plano OXY con centro el origen, de forma que su aceleración tangencial es c…') |
(→Solución) |
||
| Línea 11: | Línea 11: | ||
<center><math>a_n = \frac{|\vec{v}|^2}{R} = \frac{(v_0+a_tt)^2}{R}=\frac{a_t^2}{R}t^2+\frac{2v_0a_t}{R}t+\frac{v_0^2}{R} = At^2+B t + C</math></center> | <center><math>a_n = \frac{|\vec{v}|^2}{R} = \frac{(v_0+a_tt)^2}{R}=\frac{a_t^2}{R}t^2+\frac{2v_0a_t}{R}t+\frac{v_0^2}{R} = At^2+B t + C</math></center> | ||
| - | [[Categoría:Problemas de cinemática | + | [[Categoría:Problemas de cinemática tridimensional (GIE)]] |
[[Categoría:Problemas de cinemática de la partícula (GIE)]] | [[Categoría:Problemas de cinemática de la partícula (GIE)]] | ||
última version al 00:29 2 feb 2012
1 Enunciado
Una partícula se mueve a lo largo de una circunferencia de radio R en el plano OXY con centro el origen, de forma que su aceleración tangencial es constante. ¿Cómo varía con el tiempo la aceleración normal de este movimiento?
2 Solución
Si la aceleración tangencial es constante, quiere decir que la rapidez varía linealmente con el tiempo
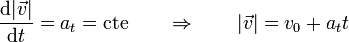
y por tanto la aceleración normal aumenta cuadráticamente con el tiempo