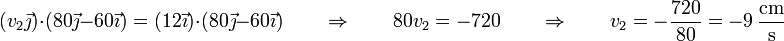Deslizamiento de una barra
De Laplace
(Página creada con '==Enunciado== Una barra metálica de 1.00 m de longitud resbala apoyada en el suelo y en una pared vertical. En un momento dado su extremo inferior se encuentra a una dis…') |
|||
| Línea 7: | Línea 7: | ||
==Velocidad del extremo== | ==Velocidad del extremo== | ||
| + | Existen numerosas maneras de determinar la velocidad del extremo superior. | ||
| + | |||
| + | En primer lugar determinamos la posición de este extremo. Siguiendo la sugerencia del enunciado, consideramos un sistema de ejes centrado en la esquina, con el eje OX en el suelo y el OZ en la pared. En este caso, la posición del extremo inferior es | ||
| + | |||
| + | <center><math>\vec{r}_1 = b\vec{\imath}=(60\vec{\imath})\,\mathrm{cm}</math></center> | ||
| + | |||
| + | y la del extremo superior es de la forma | ||
| + | |||
| + | <center><math>\vec{r}_2 = h\vec{k}</math></center> | ||
| + | |||
| + | Hallamos el valor de <math>h</math> por el teorema de Pitágoras | ||
| + | |||
| + | <center><math>b^2 +h^2 = L^2\qquad\Rightarrow\qquad h = \sqrt{L^2-b^2} = 80\,\mathrm{cm}</math></center> | ||
| + | |||
| + | Las velocidades de estos dos puntos son tangentes a las respectivas superficies de contacto | ||
| + | |||
| + | <center><math>\vec{v}_1 = v_1\vec{\imath} = (12\vec{\imath})\frac{\mathrm{cm}}{\mathrm{s}}\qquad\qquad \vec{v}_2 = v_2\vec{\jmath}</math></center> | ||
| + | |||
| + | Siendo <math>v_2</math> la cantidad que deseamos determinar. De entrada podemos decir que va a resultar una cantidad negativa, pues si el extremo inferior se aleja de la esquina, el otro debe acercarse a ella. Si no, la barra se estaría estirando. Sin embargo, no hace falta suponerlo, sino que resultará solo. | ||
| + | |||
| + | ===Por la condición de rigidez=== | ||
| + | La forma más sencilla de hallar la velocidad del extremo superior es aplicando la condición cinemática de rigidez, ya que la barra constituye un sólido rígido. Esto se expresa matemáticamente como las velocidades son equiproyectivas | ||
| + | |||
| + | <center><math>\vec{v}_2\cdot(\vec{r}_2-\vec{r}_1) = \vec{v}_1\cdot(\vec{r}_2-\vec{r}_1)</math></center> | ||
| + | |||
| + | Sustituyendo los datos conocidos | ||
| + | |||
| + | <center><math>(v_2\vec{\jmath})\cdot(h\vec{\jmath}-b\vec{\imath}) = (v_1\vec{\imath})\cdot(h\vec{\jmath}-b\vec{\imath})\qquad\Rightarrow\qquad v_2h = -v_1 b\qquad \Rightarrow\qquad v_2 = -\frac{v_1b}{h}</math></center> | ||
| + | |||
| + | con el valor numérico | ||
| + | |||
| + | <center><math>(v_2\vec{\jmath})\cdot(80\vec{\jmath}-60\vec{\imath}) = (12\vec{\imath})\cdot(80\vec{\jmath}-60\vec{\imath})\qquad\Rightarrow\qquad 80v_2 = -720\qquad \Rightarrow\qquad v_2 = -\frac{720}{80}=-9\,\frac{\mathrm{cm}}{\mathrm{s}}</math></center> | ||
| + | |||
==Posición del CIR== | ==Posición del CIR== | ||
[[Categoría:Problemas de cinemática del sólido rígido (GIE)]] | [[Categoría:Problemas de cinemática del sólido rígido (GIE)]] | ||
Revisión de 12:10 21 ene 2012
Contenido |
1 Enunciado
Una barra metálica de 1.00 m de longitud resbala apoyada en el suelo y en una pared vertical. En un momento dado su extremo inferior se encuentra a una distancia de 60 cm de la esquina y se mueve con velocidad de 12 cm/s alejándose de la esquina
- ¿Con qué velocidad se mueve el extremo superior de la barra?
- Considerando un sistema de ejes centrado en la esquina, con el suelo como eje OX y la pared como eje OZ, ¿dónde se encuentra el C.I.R. de la barra en el instante anteriormente descrito?
2 Velocidad del extremo
Existen numerosas maneras de determinar la velocidad del extremo superior.
En primer lugar determinamos la posición de este extremo. Siguiendo la sugerencia del enunciado, consideramos un sistema de ejes centrado en la esquina, con el eje OX en el suelo y el OZ en la pared. En este caso, la posición del extremo inferior es
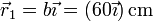
y la del extremo superior es de la forma
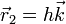
Hallamos el valor de h por el teorema de Pitágoras

Las velocidades de estos dos puntos son tangentes a las respectivas superficies de contacto
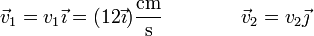
Siendo v2 la cantidad que deseamos determinar. De entrada podemos decir que va a resultar una cantidad negativa, pues si el extremo inferior se aleja de la esquina, el otro debe acercarse a ella. Si no, la barra se estaría estirando. Sin embargo, no hace falta suponerlo, sino que resultará solo.
2.1 Por la condición de rigidez
La forma más sencilla de hallar la velocidad del extremo superior es aplicando la condición cinemática de rigidez, ya que la barra constituye un sólido rígido. Esto se expresa matemáticamente como las velocidades son equiproyectivas
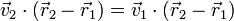
Sustituyendo los datos conocidos

con el valor numérico